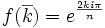Groupe fini - Définition

Théorème de Wilson

Dans un groupe abélien fini le produit des éléments est égal

• au neutre si son ordre est impair,
• au produit des involutions si son ordre est pair.

Pour le groupe , avec p premier impair, on retrouve le théorème de Wilson classique.

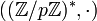
En effet, l'ordre, qui est égal à p-1, est pair et l'unique involution est la classe (modulo p) de -1.

Morphismes de groupes

Lorsque deux groupes sont isomorphes, ils sont identiques du point de vue de la théorie des groupes.

L'étude des morphismes de groupes est donc importante pour la compréhension des groupes. Des branches de la théorie des groupes finis, comme la théorie des représentations d'un groupe fini, sont consacrées entièrement à cette activité.

Par exemple, les groupes et sont isomorphes.

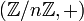
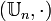
Pour le montrer, il suffit de vérifier que l'application définie par

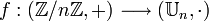
est un isomorphisme de groupe.

Dire que ces groupes sont isomorphes signifie qu'ils sont identiques : toutes les propriétés de l'un se retrouvent dans l'autre. Dans la théorie des groupes, on n'étudiera donc les propriétés que d'un seul de ces deux groupes (celui qu'on veut).

Sous-groupes de Sylow

Soit G un groupe fini d'ordre n, soit p un diviseur premier de n, soit p^r la plus grande puissance de p qui divise n, de sorte que n=p^rm, m étant un entier non divisible par p. On appelle p-sous-groupe de Sylow de G tout sous-groupe d'ordre p^r de G.

On démontre les énoncés suivants (théorèmes de Sylow) :

1. tout p-sous-groupe de G, c'est-à-dire tout sous-groupe de G dont l'ordre est une puissance de p, est contenu dans au moins un p-sous-groupe de Sylow de G ; il en résulte que les p-sous-groupes de Sylow de G sont les éléments maximaux de l'ensemble des p-sous-groupe de G, ce par quoi certains auteurs les définissent ;
2. les p-sous-groupe de Sylow de G sont conjugués entre eux ;
3. leur nombre est congru à 1 modulo p ;
4. ce nombre divise le facteur m défini plus haut.

Les sous-groupes de Sylow sont un instrument essentiel de l'étude des groupes finis.

Produit direct - Produit semi-direct

À partir de deux groupes finis H et K, on peut construire un nouveau groupe : le produit direct externe de H par K ; plus généralement, si l'on se donne en plus un morphisme , alors on peut construire le produit semi-direct externe de H par K suivant f. Ce sont des groupes finis, d'ordre |H| |K|.

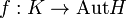
Une question naturelle se pose alors : si G est un groupe, à quelle condition G est-il un produit direct interne (ou un produit semi-direct interne) de deux sous-groupes H et K ?

Donnons un critère répondant à cette question. On pose (attention, ce sous-ensemble de G n'est en général pas un groupe).

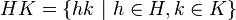
Produit direct interne

Un groupe G est produit direct interne de deux sous-groupes H et K si et seulement si :

• les groupes H et K sont distingués dans G,
• ,
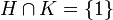
• G=HK.

Produit semi-direct interne

Un groupe G est produit semi-direct interne de deux sous-groupes H et K si et seulement si :

• le groupe H est distingué dans G,
• ,
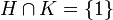
• G=HK.

Lorsque G est fini, on peut s'aider de l'égalité combinatoire suivante :

Ainsi, dans le cas où G est fini, les deux critères se voient considérablement simplifiés. En effet si les deux premiers points du critère sont vérifiés, alors le troisième point peut être remplacé par |G|=|H| |K|.

Parmi les exemples donnés ci-dessus, on peut montrer que le groupe de Klein est isomorphe au produit direct . Le groupe diédral est quant à lui isomorphe au produit semi-direct de par .

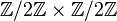
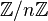
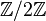
On a vu que tout groupe cyclique est abélien. Le groupe de Klein montre que la réciproque est fausse. On a cependant le résultat remarquable suivant :

Tout groupe abélien fini est un produit direct de groupes cycliques.