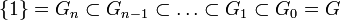Groupe fini - Définition
La liste des auteurs de cet article est disponible ici.
Bibliographie
- Jean-Pierre Serre, Groupes finis, Cours à l’École Normale Supérieure de Jeunes Filles, 1978/1979, en ligne.
- D. Gorenstein, Finite Groups, 2e édition, 1980. (Inclut la théorie des représentations.)
- H. Kurzweil et B. Stellmacher, The Theory of Finite Groups. An Introduction. Springer, 2004. (N'inclut pas la théorie des représentations.)
- I. Martin Isaacs, Finite Group Theory, Graduate Studies in Mathematics, vol. 92, American Mathematical Society, 2008. (N'inclut pas la théorie des représentations.)
Classification des groupes finis
On rencontre de nombreuses structures de groupes finis de nature très différentes. À ce titre, l'étude des groupes finis est riche et compliquée. Une approche naturelle pour aborder cette théorie serait de donner une classification des groupes finis, c’est-à-dire, une liste de familles de groupes décrivant, à isomorphisme près, tous les groupes finis. Ce problème est très ardu. On est d'ailleurs actuellement incapable de produire une telle liste.
Apportons tout de même quelques éléments de réponses. Dans le cas où le groupe est abélien, la théorie est parfaitement connue. Elle se généralise même aux groupes abéliens de type fini. Sinon, on introduit des groupes d'un type particulier : les groupes simples. On va tenter de saisir le rôle primordial qu'ils ont et comprendre comment, dans une certaine mesure, ils permettent d'appréhender la classification des groupes finis. Auparavant, on a besoin d'introduire quelques notions.
Soit G un groupe fini, on appelle suite normale de G toute suite finie strictement décroissante (au sens de l'inclusion) de sous-groupes :
telle que Gi est un sous-groupe distingué de Gi-1.
Une suite normale est dite de décomposition si elle est maximale. Le groupe Gi étant distingué dans Gi-1, il y a un sens à considérer le groupe quotient Gi-1/Gi (noté Fi dans la suite). Les groupes Fi qui apparaissent dans cette construction sont appelés les facteurs de décomposition de la suite. La maximalité de la suite de décomposition entraîne immédiatement qu'ils sont simples.
Par ailleurs, un théorème de Jordan-Hölder affirme que deux suites de décomposition de G ont (à isomorphisme près) les mêmes facteurs de décomposition. (Attention, ils peuvent ne pas apparaître dans le même ordre).
-
-
- Ainsi, à tout groupe fini G, on est capable d'associer une suite de groupes simples (F1, ... ,Fn).
-
Cette suite ne caractérise pas le groupe G (ce qui est dommage, sinon on aurait complètement ramené l'étude des groupes finis et de leur classification à celle des groupes simples ! ). Prenons pour s'en convaincre le cas du groupe cyclique à 4 éléments
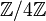
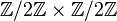
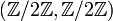
Elle a cependant une très forte influence sur sa structure. Citons par exemple l'étude des groupes résolubles (c’est-à-dire, dans le cas fini, des groupes dont les facteurs de décomposition sont des groupes cycliques d'ordre premier).
On arrive tout naturellement à une question capitale en théorie des groupes finis, connue sous le nom du problème de l'extension qui s'énonce par :
Étant donnés deux groupes finis H et K, quels sont les groupes finis G tels que
-
-
-
- H est isomorphe à un sous-groupe distingué de G (que l'on note abusivement toujours H).
-
-
-
-
-
-
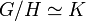
-
-
-
Les groupes G solutions de ce problème sont appelés des extensions de H par K .
Les produits directs et semi-directs sont des exemples de solutions au problème de l'extension. Cependant, toute solution du problème de l'extension ne se présente malheureusement pas sous la forme d'un produit direct ou d'un produit semi-direct. On peut le voir par exemple avec le groupe des quaternions, qui est une extension de
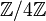
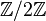
Supposons un instant que l'on sache résoudre le problème de l'extension en général. On serait alors capable de reconstruire tous les groupes finis à partir des groupes simples (en résolvant le problème de l'extension de proche en proche à partir d'une suite de groupes simples - qui deviendrait ensuite la suite de facteurs de décomposition du groupe construit).
Le problème de l'extension apparaît donc comme une sorte de réciproque à celui d'associer à un groupe fini une suite de facteurs de décomposition.
-
-
- Cette approche montre que l'étude des groupes finis revient à :
-
-
-
-
-
-
- l'étude des groupes simples ;
- le problème de l'extension.
-
-
-
-
Ainsi les groupes finis simples apparaissent comme les briques élémentaires de la théorie des groupes finis (on peut faire l'analogie avec les nombres premiers en théorie des entiers ! Attention tout de même, la suite des facteurs premiers d'un nombre entier caractérise complètement ce nombre, ce qui n'est pas le cas des groupes simples pour les groupes finis comme on vient de le voir ! )
En 1981, après plus d'un demi-siècle de travail acharné et quelques milliers de pages de démonstration, la communauté mathématique donne une classification des groupes simples finis. Plus précisément, tout groupe simple fini appartient à l'une des familles suivantes :
-
-
-
- les groupes cycliques dont l'ordre est un nombre premier.
-
-
-
-
-
- les groupes de Chevalley.
-
-
-
-
-
- les groupes alternés
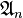
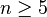
- les groupes alternés
-
-
-
-
-
- les groupes sporadiques, au nombre de 26.
-
-