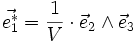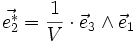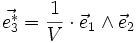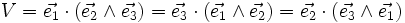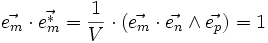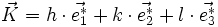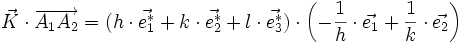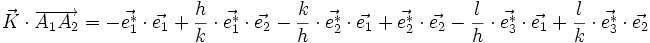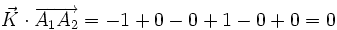Indices de Miller et indices de direction - Définition

Espace réciproque et diffraction

Considérons l'espace réciproque, c'est-à-dire l'espace vectoriel formé par les vecteurs d'onde ; l'utilisation de cet espace permet de déterminer facilement les conditions de diffraction (voir aussi l'article Théorie de la diffraction sur un cristal).

On y définit la base réciproque par :

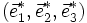
où V est le volume de la maille qui peut s'écrire :

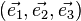
D'après les propriétés du produit vectoriel, on a :

, soit et

, soit et

, soit et

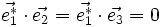
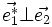
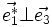
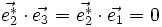
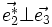
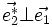
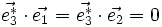
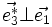
Par ailleurs, si (m, n, p) est une permutation circulaire de (1, 2, 3), on a :

Notons le vecteur ayant les coordonnées (h, k, l) dans cette base réciproque :

alors ce vecteur est normal au plan (hkl) : si ni h, ni k, ni l ne sont nuls, alors

soit

donc

donc . On peut démontrer de même que et que . Le est perpendiculaire à deux vecteurs non colinéaires du plan, il est donc normal au plan. Si h, k ou l est nul, on montre l'orthogonalité en se basant sur le fait qu'un ou deux des axes est parallèle au plan.

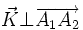
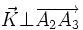
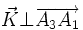
Or, les vecteurs ayant des coordonnées entières dans la base réciproque correspondent aux conditions de diffraction. Ainsi :

• dans le cas de la diffraction sur un monocristal (cliché de Laue, microscopie électronique en transmission), on peut associer une tache de diffraction à un plan cristallographique ;
• dans le cas d'une poudre (chambre de Debye-Scherrer, diffractomètre Bragg-Brentano), on peut associer un anneau de Debye ou un pic de diffraction à un plan cristallographique.

On parle ainsi de tache, d'anneau ou de pic (hkl). Cette association s'appelle « l'indexation ».