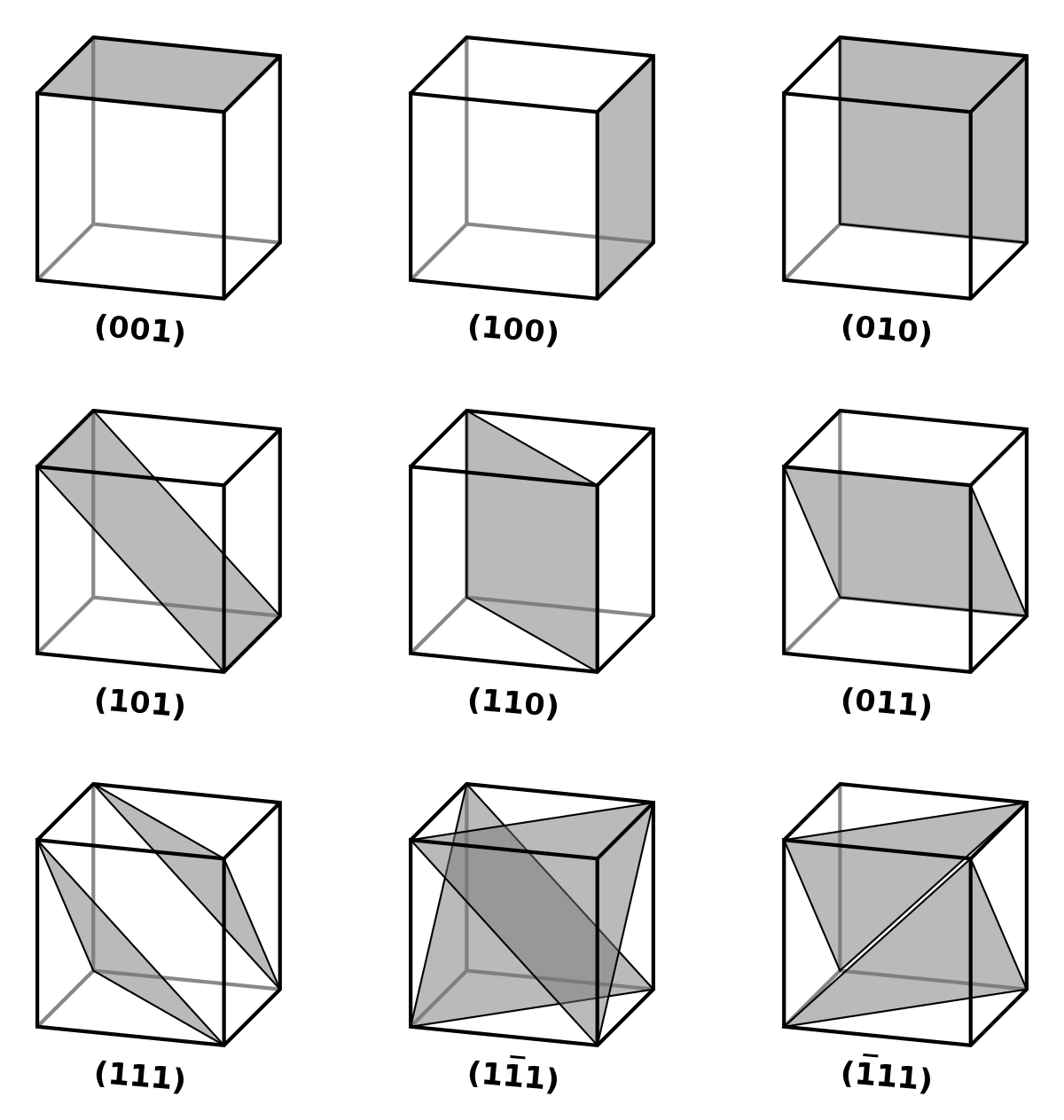
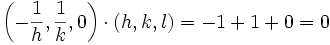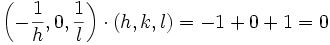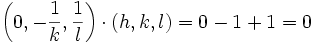Indices de Miller et indices de direction - Définition

Introduction

Les indices de Miller sont une manière de désigner les plans dans un cristal. On utilise des indices similaires pour désigner les directions dans un cristal, les indices de direction.

Un cristal est un empilement ordonné d'atomes, d'ions ou de molécules, appelés ci-après « motifs ». La périodicité du motif est exprimée par un réseau constitué de nœuds qui représentent les sommets de la maille. Les plans et directions sont qualifiés de « nodaux » (plan nodal, direction nodale) ou mieux encore « réticulaire ». Une direction réticulaire est dite rangée.

En métallurgie, on travaille fréquemment avec des cristaux constitués d'un seul type d'atomes ; on parle donc de « plan atomique », de « direction atomique » ou de « rangée d'atomes », mais ce ne sont que des cas particuliers.

Les arêtes de la maille conventionnelle définissent les vecteurs de la base.

Importance des plans et directions denses

Plan cristallographique et densité atomique
bas : cristal de profil
haut : vues selon un axe perpendiculaire à chaque surface

Le cristal n'est pas isotrope, il n'y a pas de raison que ses propriétés le soient. Les lignes et plans de grande densité vont présenter des propriétés particulières :

• optiques : la propagation d'une onde lumineuse dans le cristal (réfraction) se fait par diffusion Rayleigh de proche en proche, entre les atomes ; la vitesse de propagation peut donc différer selon la densité de la direction, provoquant le phénomène de biréfringence ;
• liées à la tension superficielle : si le matériau se condense sous la forme d'un cristal, c'est qu'un motif est plus stable lorsqu'il est entouré d'autres motifs ;
  • propagation d'une fissure et plan de clivage : les motifs d'une surface libre sont exposés à l'air ; la surface libre est plus stable si elle correspond à un plan de grande densité, car alors chaque motif est entouré d'un maximum de motifs ;
  • forme d'un pore, pour la même raison que ci-dessus ;
• adsorption et réactivité : le nombre de sites d'adsorption, et donc la réactivité chimique, dépend de la densité d'atomes ;
• dislocations
  • le cœur d'une dislocation va plus s'étendre dans un plan dense, cela réduit le frottement lors du déplacement de la dislocation (force de Peierls-Nabarro au cours de la déformation plastique) ; les glissements se font donc préférentiellement selon des plans denses ;
  • la perturbation que représente une dislocation (vecteur de Burgers) est une direction dense : en effet, un décalage d'un motif dans une direction dense représente une ditorsion faible (les motifs étant rapprochés) ;
  • la ligne d'une dislocation va également tendre à être une direction dense, afin de diminuer la tension de ligne (une boucle de dislocation aura donc tendance à être un polygone).

Repérage d'un plan

Définition des indices de Miller d'un plan.

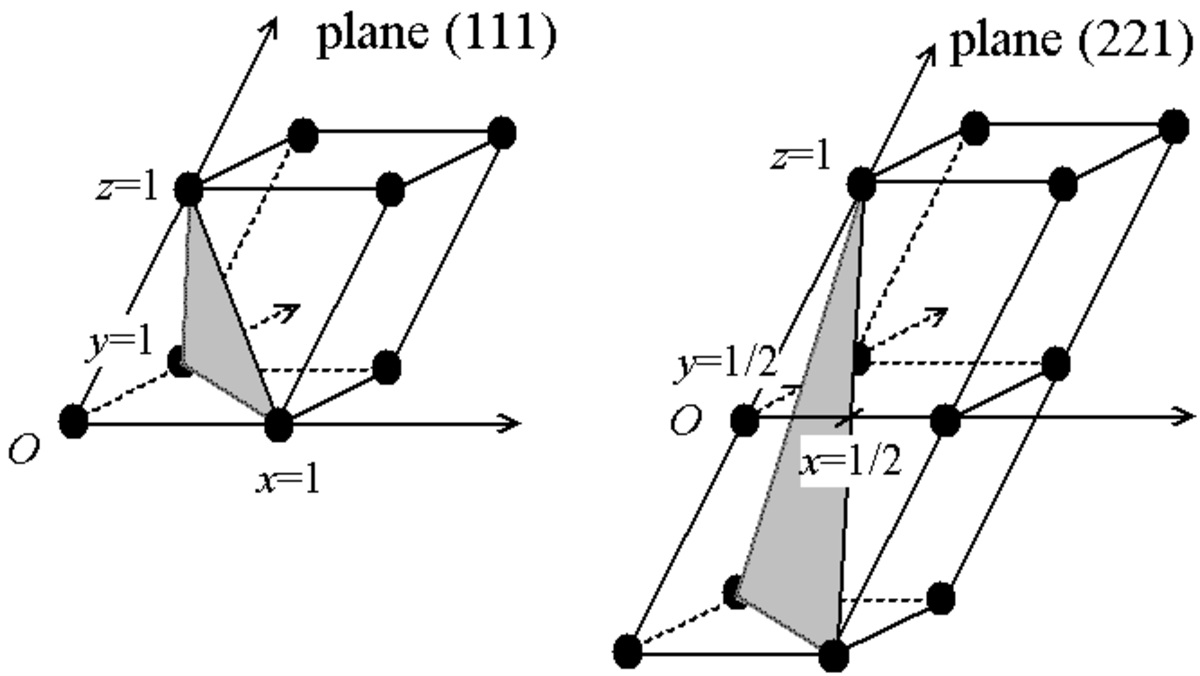
Considérons le plan le plus proche de l'origine mais qui ne passe pas par l'origine. Si l'on prend l'intersection de ce plan avec les trois axes, on obtient les trois coordonnées de trois points :

• (P,0,0) l'intersection du plan avec l'axe des x ;
• (0,Q,0) l'intersection du plan avec l'axe des y ;
• (0,0,R) l'intersection du plan avec l'axe des z ;

alors l'inverse des coordonnées des intersections donne les indices de Miller, avec la convention 1/∞ = 0 (l'indice est 0 si l'axe est parallèle au plan). Ces indices sont notés entre parenthèse (hkl ) :

• h = 1/P ;
• k = 1/Q ;
• l = 1/R.

Exemples de plans pour une structure cubique.

Si ni h, ni k, ni l ne sont nuls, alors le plan passe donc par les points A₁ (1/h,0,0), A₂ (0,1/k,0), A₃ (0,0,1/l ), donc les vecteurs suivants sont dans le plan :

•  ;
•  ;
• .

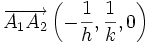
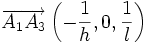
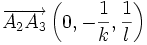
Ces vecteurs n'étant pas colinéaires, deux de ces vecteurs forment une base du plan.

Si un des indices est nul, alors un des vecteurs de la base de la maille est aussi un vecteur du plan, celui dont la composante non nulle est l'indice nul du plan :

• si h = 0, le vecteur [1 0 0] (vecteur de coordonnées (1,0,0)) est dans le plan ;
• si k = 0, le vecteur [0 1 0] est dans le plan ;
• si l = 0, le vecteur [0 0 1] est dans le plan.

Si la base est orthonormale, le produit scalaire du vecteur [hkl ] avec ces vecteurs est nul :

Donc dans le cas d'un réseau cubique, le vecteur [hkl ] est perpendiculaire à la surface, c'en est un vecteur normal. Dans le cas général, il faut changer de base pour que le vecteur de coordonnées (h, k, l ) soit perpendiculaire au plan (cf. ).