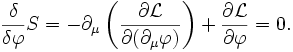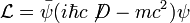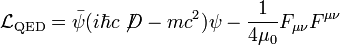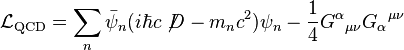Lagrangien - Définition
La liste des auteurs de cet article est disponible ici.
Lagrangiens et densités de lagrangien dans la théorie des champs
Dans la théorie des champs, on distingue parfois le lagrangien L, dont l'intégrale sur le temps est l'action :
et la densité lagrangienne
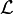
Le lagrangien est ainsi l'intégrale spatiale de la densité lagrangienne. Cependant, on appelle souvent
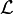
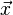
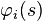
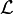
Formalisme mathématique
Soit M une variété de dimension n, et une variété de destination T. Soit
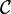
Avant tout donnons quelques exemples :
- En mécanique classique, dans le formalisme d'Hamilton, M est le variété de dimension 1

- Dans la théorie des champs, M est la variété espace-temps et l'espace de destination est l'ensemble des valeurs possibles des champs en chaque point. Si par exemple il y a m champs scalaires réels φ1,...,φm, alors la variété de destination est
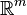

Supposons maintenant qu'il existe une fonctionnelle
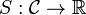


Pour que l'action soit locale, nous avons besoin de restrictions supplémentaires sur l'action. Si
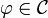
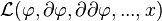
La plupart du temps, on impose que le lagrangien dépende uniquement de la valeur des champs, de leur dérivées premières, mais pas des dérivées d'ordre supérieur. C'est en fait seulement par commodité, et ce n'est pas vrai en général. Nous le supposons cependant dans le reste de cet article.
Fixons des conditions aux limites, essentiellement la donnée de φ aux frontières si M est compact, ou une limite pour φ quand x tend vers l'infini (ce qui est pratique lors d'intégrations par parties). Le sous-espace de
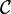
La solution est donnée par les équations d'Euler-Lagrange (en utilisant les conditions aux limites) :
On retrouve la dérivée fonctionnnelle par rapport à φ de l'action dans le membre de gauche.
Lagrangiens en théorie quantique des champs
Le lagrangien de Dirac
La densité lagrangienne pour un champ de Dirac est:
où ψ est un spineur,
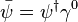
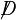
Le lagrangien de l'électrodynamique quantique
La densité lagrangienne en QED est:
où Fμν est le tenseur électromagnétique.
Le lagrangien de la chromodynamique quantique
La densité lagrangienne en QCD est [1] [2] [3]
où D est la dérivée covariante de jauge en QCD, et Gαμν est le tenseur de la force du champ du gluon.
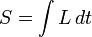
![S [\varphi_i] = \int{\mathcal{L} [\varphi_i (x)]\, d^4x}](https://static.techno-science.net/illustration/Definitions/autres/e/e4f526bbf4b6bda0d1d694eadd7675c9_18163e673b1d2120b02067ebf2dca2a1.png)
![\forall\varphi\in\mathcal{C}\, S[\varphi]\equiv\int_M d^nx \mathcal{L}(\varphi(x),\partial\varphi(x),\partial\partial\varphi(x), ...,x).](https://static.techno-science.net/illustration/Definitions/autres/8/8842702deb6e823fd032233b7638c950_9644eed6a1165211cfc747fb9a648f1c.png)