Dérivée covariante - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En géométrie différentielle, la dérivée covariante est un outil destiné à obtenir la dérivée d'un champ vectoriel sur une variété.
Il n'existe pas de différence entre la dérivée covariante et la connexion, à part la manière dont elles sont introduites.
Dans la théorie des variétés riemanniennes et pseudo-riemanniennes, la dérivée covariante est souvent utilisée pour la connexion de Levi-Civita.
Dans cet article, on définit la dérivée covariante (aussi connue sous le nom de dérivée de tenseur) d'un vecteur au sein d'un champ vectoriel. La dérivée covariante d'un tenseur est une extension de ce concept.
L'ensemble de cet article utilise la convention de sommation d'Einstein pour les tenseurs et les coordonnées covariantes et contravariantes. Le lecteur est supposé avoir des notions de variétés et particulièrement du vecteur tangent.
Concept général
La dérivée covariante

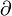
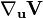
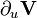
Dans le cas d'un espace euclidien disposant d'un système de coordonnées orthonormées, on peut définir la dérivée d'un champ de vecteur en tant que différence entre deux vecteurs en deux points proches. Dans un tel système il est possible de translater un des vecteurs à l'origine de l'autre, parallèlement à lui-même. On obtient l'exemple le plus simple de dérivée covariante, obtenue en prenant la dérivée des coordonnées.
Dans le cas général, cependant, il est nécessaire de prendre en compte le changement du système de coordonnées. Par exemple, si la même dérivée covariante devait être écrite en coordonnées polaires dans un espace euclidien à deux dimensions, elle devrait contenir un terme supplémentaire décrivant la rotation des coordonnées elles-mêmes. Dans d'autres cas les termes supplémentaires décrivent comme les coordonnées s'étendent, se contractent, se déforment, ...
Un vecteur le long d'une courbe paramétrique t est exprimé dans un système de coordonnées
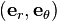
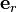
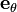
Il est préférable de ne pas identifier t au paramètre temps, du moins pour les applications en relativité générale : c'est simplement un paramètre variant continûment et de manière monotone le long de la courbe. (Voir courbe paramétrique).
En espace courbe, tel que la surface de la Terre, la translation n'est pas définie, et son analogie, le transport parallèle, dépend du chemin le long duquel le vecteur est translaté.
Soit un vecteur e défini sur l'équateur d'une sphère en un point Q et dirigé vers le Nord. Supposons qu'on transporte parallèlement tout d'abord le vecteur le long de l'équateur jusqu'à P, puis (toujours grâce au transport parallèle le long d'un méridien) vers le pôle nord et enfin à nouveau jusqu'au point Q le long d'un autre méridien. On remarque que le transport parallèle de ce vecteur le long d'un circuit fermé ne retourne pas le même vecteur. A la place, il a pris une autre orientation. Ceci ne pourrait arriver dans l'espace euclidien et est causé par la courbure de la surface du globe. Le même effet peut être observé si on déplace le vecteur le long d'une surface infinitésimale. Le changement infinitésimal du vecteur est une mesure de la courbure.
Notes
Les vecteurs u et v dans la définition sont définis en un même point P. De même la dérivée covariante
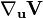
La définition de la dérivée covariante n'utilise pas la métrique de l'espace. Cependant, une métrique définit de manière unique une dérivée covariante appelée la connexion de Levi-Civita.
Les propriétés de la dérivée impliquent que
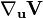
La dérivée covariante peut être décrite comme un tenseur dans un système de coordonnées donné, mais ce n'est pas un tenseur dans la mesure où elle n'est pas invariante par changement de coordonnées.
L'information sur le voisinage du point P dans la dérivée covariante peut être utilisée pour définir le transport parallèle d'un vecteur. De même la courbure, la torsion et les géodésiques peuvent être définies uniquement en termes de dérivée covariante.

















































