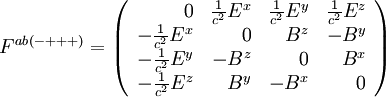Tenseur électromagnétique - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
sur les tenseurs
Tenseur
Tenseur (mathématiques)
Produit tensoriel
... de deux modules
... de deux applications linéaires
Algèbre tensorielle
Champ tensoriel
Espace tensoriel
Convention d'Einstein
Tenseur métrique
Tenseur énergie-impulsion
Tenseur de Riemann
... de Ricci
... d'Einstein
... de Weyl
... de Levi-Civita
... de Killing
... de Killing-Yano
... de Bel-Robinson
... de Cotton-York
Tenseur électromagnétique
Tenseur des contraintes
Tenseur des déformations
Modules
Algèbre extérieure
Le tenseur électromagnétique, ou tenseur de Maxwell est le nom de l'objet mathématique (un tenseur) décrivant la structure du champ électromagnétique en un point donné.
Définition
Ce tenseur est défini dans le cadre du formalisme mathématique de la relativité restreinte, où aux trois dimensions spatiales est adjointe une dimension temporelle. Les objets vectoriels ont ainsi quatre composantes, on parle donc de quadrivecteur. Le tenseur électromagnétique peut être vu comme une matrice 4×4, dont les éléments sont déterminés par un quadrivecteur appelé potentiel vecteur, habituellement noté A. Le tenseur de Maxwell, habituellement noté F est donné par la formule
-
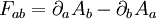
Ce tenseur est antisymétrique et de trace nulle.
Tenseur dual
Le tenseur électromagnétique étant antisymétrique, il s'agit d'un bivecteur. Il est possible d'en déduire son bivecteur dual, F*, par la formule
-
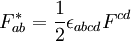
où ε est le tenseur de Levi-Civita, ce qui donne
-
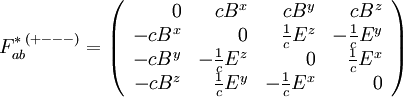
et
-
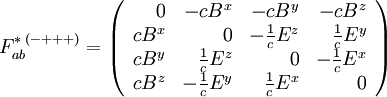
Dans les deux cas, l'opération de dualisation permet de transformer le champ électrique E en cB et le champ magnétique B en -E/c.
Expression des composantes
Le tenseur électromagnétique permet de reconsidérer la force de Lorentz s'exerçant sur une particule chargée. Cette force, f a pour expression
-
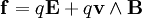
En relativité restreinte, son expression devient
- fa = qFabub,
où u est la quadrivitesse de la particule considérée. Ceci permet de reconstituer les composantes du tenseur de Maxwell dans un système de coordonnées cartésiennes :
-
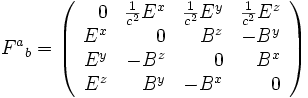
L'expression des composantes F dépend de la convention de signature de la métrique utilisée. Dans l'hypothèse où celle-ci est du type (+---), on a
-
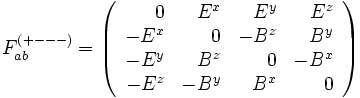
Dans le cas inverse, avec la convention (-+++), on a
-
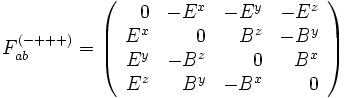
La différence entre ces deux notations disparaît si l'on exprime les champs électrique E et magnétique B en fonction du potentiel vecteur. L'expression de F correspond à
-
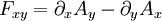
Dans la convention (-+++), cela correspond aussi à
-
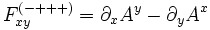
Cette expression correspond à la composante selon z du rotationnel tridimensionnel de A, qui correspond, d'après les équations de Maxwell à Bz, conformément à l'expression de F dans la convention (-+++). De même, dans la convention (+---), on a
-
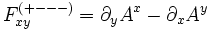
qui correspond d'après ce qui précède à -Bz. De façon similaire, on a
-
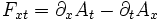
En convention (-+++), ceci s'écrit
-
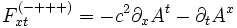
et correspond donc à la composante de E selon x, si l'on assimile le potentiel électrique V à c2At, alors qu'en convention (+---), on a
-
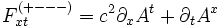
qui correspond bien à -Ex.
Les composantes contravariantes s'expriment de la même façon :
-
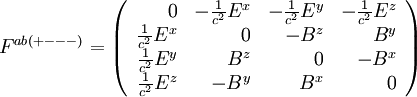
et
-