Lemme d'Urysohn - Définition

Introduction

Le mathématicien Pavel Urysohn donne son nom au lemme de l'article.

Le lemme d'Urysohn est un résultat de topologie, qui établit que pour deux fermés disjoints A et B d'un espace normal X, il existe une fonction continue de X dans l'intervalle [0, 1] qui vaut 1 sur A et 0 sur B. On le considère parfois comme le « premier résultat non trivial sur les espaces topologiques ».

Ce lemme est utilisé pour établir des résultats topologiques fins, comme le théorème de Jordan, qui indique qu'un lacet sépare l'espace en deux composantes connexes.

Ce lemme permit d'étendre aux espaces normaux le théorème de prolongement de Tietze, initialement démontré en 1914 par Heinrich Tietze pour les espaces métriques. Pavel Urysohn trouve une nouvelle démonstration et énonce son lemme un peu plus tard, dans un texte mathématique dont l'objectif est la démonstration des théorèmes sur l'invariance de la dimension d'un espace topologique localement homéomorphe à un espace euclidien.

Énoncés

Il existe un premier énoncé spécifique aux espaces normaux :

• Un espace topologique séparé X est normal si et seulement si, pour tous fermés disjoints A et B de X, il existe une fonction continue f de X dans l'intervalle [0, 1], qui vaut 1 sur A et 0 sur B.

Ce théorème est fréquemment utilisé sous la forme du corollaire suivant :

• On suppose ici que X est un espace localement compact et que K désigne un compact de X. Il existe une application continue f, définie sur X, à valeurs dans [0, 1] à support compact, qui vaut 1 sur K.

Ce lemme est aussi utilisé en géométrie différentielle. Il devient utile de trouver une fonction f infiniment différentiable, d'où l'existence de l'énoncé suivant :

• Soit K un compact d'un espace euclidien E et Ω un ouvert de E contenant K. Il existe une fonction de E dans [0, 1], infiniment différentiable qui vaut 1 sur K et dont le support est inclus dans Ω.

Démonstrations topologiques

Lemme

La démonstration proposée ici s'appuie sur les fractions dyadiques.

• Si, pour tous fermés A et B disjoints, il existe une fonction continue f de X dans l'intervalle [0, 1], qui vaut 1 sur A et 0 sur B, l'espace X est normal :

Les ensembles f^-1([0, 1/2[) et f^-1(]1/2, 1]) sont les deux ouverts recherchés.

• Réciproque :

Soit D l'ensemble fractions dyadiques comprises entre 0 et 1, c'est-à-dire des rationnels de la forme k/2ⁿ, n étant un entier positif ou nul et k un entier variant de 0 à 2ⁿ. Pour tout r élément de D, on définit un ouvert U(r) tel que :

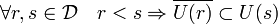
On procède pour cela par récurrence. Utilisant le caractère normal de l'espace topologique, soit U(0) un ouvert tel que B est inclus dans U(0) et l'adhérence de U(0) est incluse dans U(1), où U(1) désigne le complémentaire de A.

Si les U(r) sont construits pour tout r ayant un dénominateur inférieur ou égal à 2^n-1, considérons k impair. Par hypothèse de récurrence :

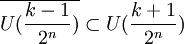
Une fois encore, l'hypothèse de normalité permet de définir un ouvert U(k/2ⁿ) tel que :

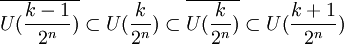
On définit une fonction f de X dans [0, 1] tel que si x est élément de A, f(x) = 1 et sinon :

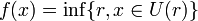
Par construction, f est égale à 1 sur A et à 0 sur B et est à valeurs dans [0,1]. Enfin, f est continue en tout point x. En effet, soit ε un réel strictement positif, x un élément de X, s et t deux éléments de D tels que f(x) = r et :

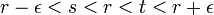
(Si r = 0, on prend s = 0, et si r = 1, on prend t = 1). La différence entre l'ensemble U(t) et l'adhérence de U(s) est un voisinage ouvert de x dont l'image par f est incluse dans [s,t]. (Si r = 0 on prend seulement U(t), et si r = 1, on prend seulement le complémentaire de l'adhérence de U(s)). La démonstration de la continuité de f complète la preuve.

Corollaire

Soit K une partie compacte d'un espace localement compact X. L'objectif est de montrer l'existence d'une fonction f continue, à support compact, qui vaut 1 sur K. Puisque X est localement compact, pour tout point k de K, il existe un ouvert U_k contenant k et dont l'adhérence est compacte. La famille (U_k) forme un recouvrement ouvert du compact K, donc il est possible d'en extraire un sous-recouvrement fini (U_kn). L'union des U_kn est un ouvert U contenant K et dont l'adhérence L est compacte donc normale. Le lemme d'Urysohn montre qu'il existe une fonction f_L, qui vaut 1 sur K et 0 sur le complémentaire de U dans L. On prolonge f_L par une fonction f, définie sur X et qui vaut 0 sur le complémentaire de L dans X. La fonction f est continue sur le fermé L, et nulle donc continue sur le complémentaire de U dans X. Elle est donc continue sur l'union X de ces deux fermés. Le support de la fonction f est un fermé du compact L, la fonction f est donc à support compact.