Lemme d'Urysohn - Définition

Approche qualitative

Fragment d'histoire

Une des grandes questions qui se posent au début du XX^e siècle en topologie est la classification des différents espaces. Un invariant important pour ce classement est la dimension. Si un espace topologique connexe possède en tout point un ouvert, contenant ce point et homéomorphe à un ouvert d'un espace euclidien, tous les espaces euclidiens ont la même dimension et cette dimension est unique. Si ce résultat est très intuitif : si un espace topologique est de même nature qu'une courbe, ce n'est alors pas un plan, la démonstration est difficile. Depuis Peano, la connaissance d'une fonction continue et surjective de R dans [0, 1]² illustre un des écueils à éviter, pour trouver des démonstrations rigoureuses.

Heinrich Tietze travaille sur cette question et, dans ce contexte, montre en 1914 que si f est une application continue définie sur un fermé d'un espace métrique, elle est continument prolongeable sur l'espace entier. Il trouve la définition d'espace normal en 1923. Pavel Urysohn, un mathématicien russe, parvient à démontrer le théorème clé de la dimension qu'il publie en 1924. Il retrouve des résultats déjà démontrés par Luitzen Brouwer en 1912, mais qu'Urysohn ne connaissait pas. Cette publication contient le lemme de l'article.

On doit encore à Tietze aussi le théorème de prolongement, qui porte maintenant son nom et dont le lemme de l'article n'est qu'un cas particulier. J. Dieudonné développe l'usage du théorème en géométrie différentielle et développe simultanément et indépendamment avec Salomon Bochner la notion de partition de l'unité en 1937. Il introduit aussi la définition d'espace paracompact en 1944, elle remplace souvent celle d'espace normal, qui contient trop d'exceptions pathologiques pour être véritablement fertile en topologie algébrique.

Démonstration intuitive

Intuitivement, il n'est pas très difficile d'imaginer une démonstration, se fondant sur la notion d'oscillation d'une fonction. L'oscillation d'une fonction f, définie sur un espace topologique et à valeurs dans un espace métrique, en un point x, est la borne inférieure des diamètres des images des voisinages de x. Si l'oscillation est nulle, la fonction est continue.

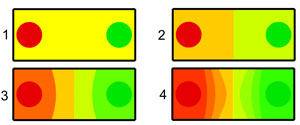
On suppose que les deux fermés A et B sont illustrés en rouge et vert sur la figure de droite. On peut définir une fonction f₁ qui vaut 1 sur A, 0 sur B et 1/2 partout ailleurs. Cette fonction est illustrée sur le graphique numéroté 1 (le jaune est la couleur milieu entre le rouge et le vert). L'axiome définissant un espace topologique normal montre qu'il existe un ouvert A₁₁ contenant A et tel que son adhérence soit strictement incluse dans le complémentaire de B, car le complémentaire de B est un ouvert contenant A. Il est alors possible de définir la fonction f₂ comme valant 1 sur A, 0 sur B 1/2 sur la frontière de A₁₁, 3/4 sur le complémentaire de A dans A₁₁ et 1/4 ailleurs. Cette fonction est représentée dans l'illustration numérotée 2. Cette fois-ci, l'oscillation de la fonction ne dépasse pas 1/4.

En réitérant la démarche, on obtient une fonction f₃ dont l'oscillation ne dépasse pas 1/8 puis une fonction (numéroté 3). En prolongeant la démarche, on obtient une fonction f_n dont l'oscillation ne dépasse pas 2 ^-n. Les fonctions deviennent de plus en plus continues, même si aucune ne l'est vraiment. Graphiquement, cela se traduit par le fait que le dégradé de couleur entre A et B est de plus en plus lisse.

La suite (f_n) converge uniformément, elle admet donc une limite f car l'intervalle [0, 1] est complet. Cette limite devrait satisfaire les hypothèses du lemme.

Usages

On trouve le lemme d'Urysohn dans deux contextes géométriques différents.

• En topologie algébrique, ce lemme est utilisé pour établir des résultats topologiques fondamentaux. Ainsi l'une des démonstrations du théorème de Jordan utilise le théorème de prolongement de Tietze, qui est un corollaire du lemme d'Urysohn.

• En géométrie différentielle, le lemme d'Urysohn est utilisé pour établir un des outils les plus importants de la géométrie différentielle. Cet outil porte le nom de partition de l'unité. Il permet par exemple d'établir l'existence d'une densité sur une variété différentielle.