Lemme d'Urysohn - Définition
La liste des auteurs de cet article est disponible ici.
Démonstrations différentielles
Fonction plateau
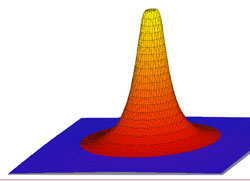
Dans toute la suite de l'article E désigne un espace euclidien et n sa dimension. La démonstration du lemme d'Urysohn en géométrie différentielle demande la construction de fonctions plateau, analogue à celle illustrée sur la figure de droite. On cherche une application fδ, où δ est un réel strictement positif, de E et à valeurs dans les nombres réels positifs, à support dans la boule fermée de centre le vecteur nul et de rayon δ, infiniment différentiable et d'intégrale sur E égale à 1.
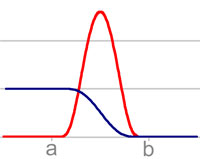
Pour construire une telle fonction, on bâtit d'abord la fonction illustrée en rouge sur la figure de gauche. Soit a et b deux nombres réels tels que a < b, on cherche à construire une application φab définie sur R, à support égal à [a, b], infiniment dérivable et à valeurs dans les nombres réels strictement positifs. On définit la fonction φab par :
![\forall x \in [-\infty, a] \cup [b, \infty],\; \varphi_{ab}(x) = 0 \quad\text{et}\quad \forall x \in ]a,b[,\; \varphi_{ab}(x) = \exp \left(\frac {-1}{(x-a)(b-x)}\right)](https://static.techno-science.net/illustration/Definitions/autres/d/daabc49698edab2b962bb31ae211927c_9c85f1ed9d11de165736ac7aab5fc427.png)
Une rapide vérification montre que φab est bien infiniment dérivable, à support égal à [a, b] et à valeurs positives. Comme elle est à valeurs strictement positives sur ]a, b[, l'intégrale dont la valeur est notée k-1 est bien différente de 0.
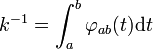
On cherche alors à construire la fonction illustrée en bleu sur la figure de gauche. C'est une fonction ψab de R dans l'intervalle [0, 1] qui vaut 1 pour toute valeur inférieure à a, 0 pour toute valeur supérieure à b et qui est infiniment dérivable. Pour la construire, il suffit de considérer la primitive de la fonction -k.φab qui vaut 0 en b. La fonction fδ est alors définie par :
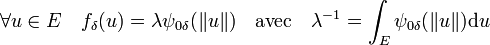
Lemme
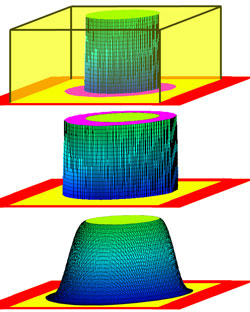
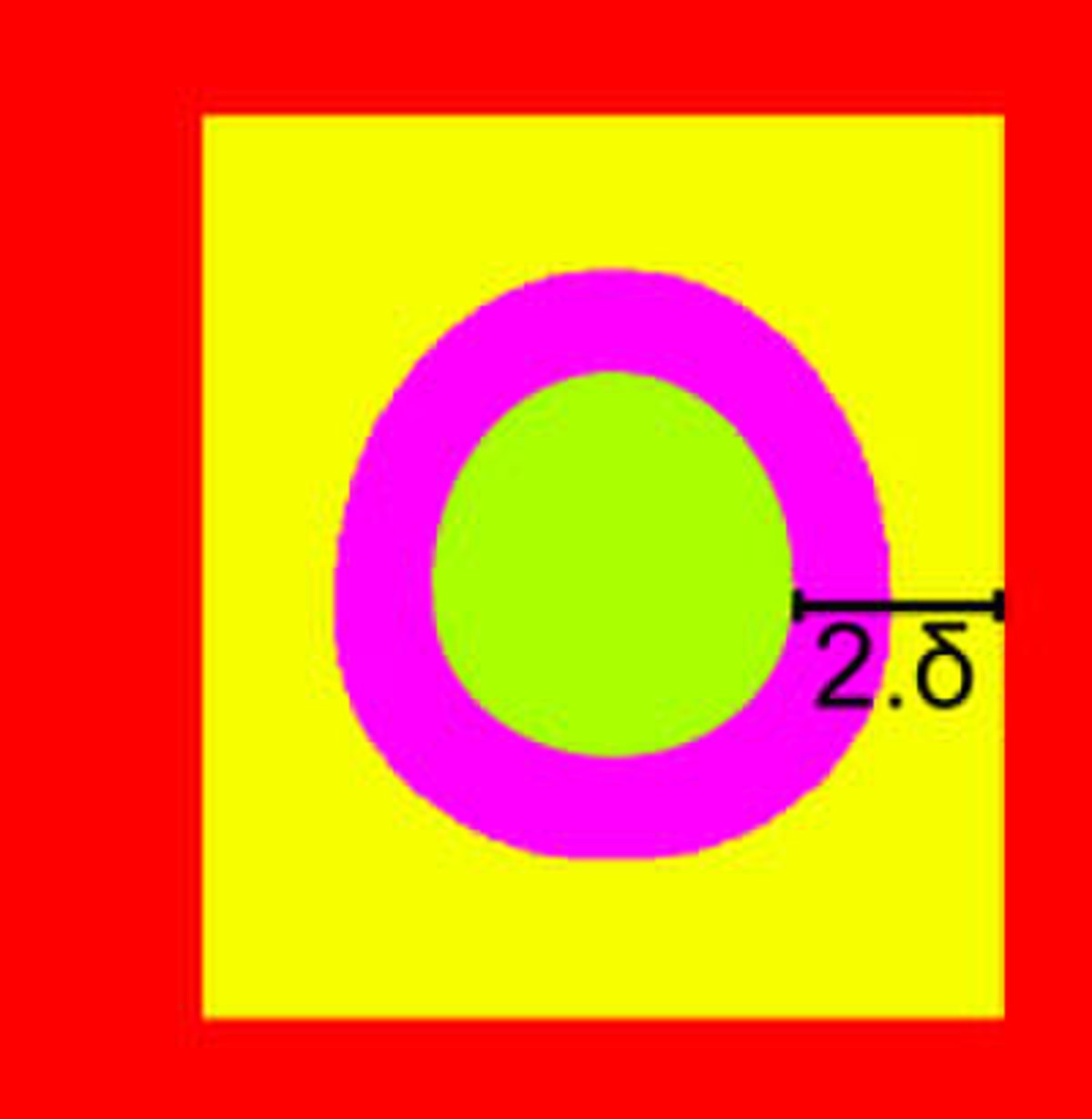
On suppose que E est un espace euclidien, K, illustré en vert sur la figure de gauche est un compact, Ω est un ouvert contenant K, en jaune sur la figure et on note cΩ, en rouge, le fermé complémentaire de Ω. L'objectif est de construire une application définie sur E, à valeurs dans [0, 1], qui vaut 1 sur K, 0 sur cΩ et infiniment différentiable. Cela revient à dire que la fonction g recherchée possède un graphe inclus dans la cage jaune de la figure en haut à droite (sauf sur la zone rouge où elle est nulle) et qu'elle recouvre le graphe de la fonction caractéristique que K, illustrée en bleu-vert sur la même figure. En termes plus mathématiques on obtient, si χK et χΩ désignent les fonctions caractéristiques de K et de Ω :
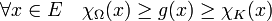
Considérons la fonction de K dans R+, qui à x associe la distance entre x et cΩ. C'est une fonction continue, définie sur un compact, elle atteint sa borne inférieure. Si cette borne inférieure était nulle, elle serait atteinte en un point x adhérent à K et à cΩ. Comme ces deux ensembles sont fermés, x serait élément de K et de cΩ. Par définition de Ω, un tel point ne peut exister et la borne inférieure est strictement positive. Soit δ un réel strictement positif tel que 2.δ soit plus petit que cette borne inférieure (illustré sur la figure de gauche). On considère alors l'ensemble V, illustré en violet sur la figure de gauche, des points de E situés à une distance inférieure ou égale à δ de K. Par construction, tout point de cΩ est à une distance au moins égale à δ de V et toute boule de centre un point de K et de rayon δ est incluse dans l'ensemble V.
On considère la fonction caractéristique χV de l'ensemble V, illustrée sur la figure au milieu à droite et on définit g comme le produit de convolution de la fonction χV et fδ du paragraphe précédent :
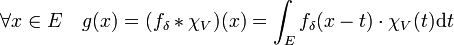
Comme les deux fonctions sont à support compact, l'intégrale est bien définie. Comme fδ est une fonction infiniment différentiable, la fonction g l'est. Comme la fonction caractéristique est à valeurs positives comprises entre 0 et 1 et que fδ est une fonction positive, d'intégrale sur E égal à 1, la fonction g prend ses valeurs dans l'intervalle [0, 1]. Si x est un élément de K, la fonction qui à t associe fδ(x - t) est partout nulle, sauf sur la boule de centre x et de rayon δ. Si x est élément de K, cette boule est incluse dans V, on en déduit :
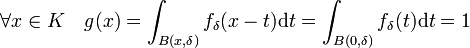
Si x est élément de cΩ, la fonction qui à t associe fδ(x - t) est encore partout nulle, sauf sur la boule de centre x et de rayon δ. Sur cette boule, la fonction χV est nulle, on en déduit que sur le complémentaire de Ω, la fonction g est bien nulle. Cette remarque termine la démonstration. La fonction g est celle illustrée sur la figure en bas à droite.