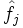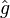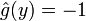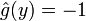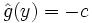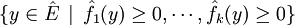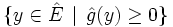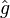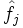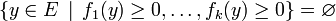Lemme de Farkas - Définition
La liste des auteurs de cet article est disponible ici.
Déduction d'inéquations en géométrie affine
La simple reproduction du résultat écrit plus haut en géométrie vectorielle serait inexacte en géométrie affine. L'énoncé est en effet faux pour les systèmes d'inéquations inconsistants. Donnons tout de suite un exemple : dans R2 où on note (u,v) le point courant, soit le système formé des deux inéquations : u-1 ≥ 0 et -u ≥ 0. Ce système est inconsistant, faux en tout point, et implique donc (au sens précis de "implique" en calcul propositionnel) n'importe quelle inéquation, par exemple l'inéquation v-3 ≥ 0. Pourtant il n'est bien sûr pas question de produire celle-ci par des manipulations algébriques simples à partir du système initial.
Un énoncé général nécessite ainsi une hypothèse supplémentaire de consistance du système.
« Lemme de Farkas généralisé » — Soient f1, ... , fk et g des formes affines sur un espace vectoriel affine de dimension finie E. On suppose l'ensemble
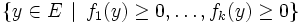
si et seulement si
- g est somme d'une combinaison linéaire à coefficients positifs ou nuls de f1, ... , fk et d'une constante positive ou nulle.
Comme dans la démonstration précédente l'implication montante est évidente. On montre l'autre, en supposant tout d'abord que
-
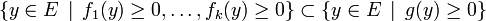
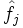
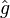
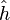
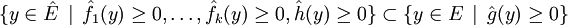
pour un point y de l'ensemble de gauche, on discute selon la valeur de
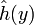
- si
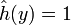
- plus généralement, si
, on se ramène au cas précédent par homothétie de rapport strictement positif ; - si
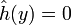
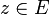
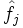
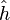
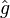
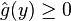
Il ne reste plus qu'à appliquer le lemme de Farkas dans sa version vectorielle pour conclure que
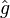
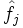
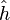
Le lemme de Farkas comme critère d'inconsistance
On dira qu'un système d'inéquations est inconsistant lorsqu'il n'a aucune solution. Si on revient à la version du théorème pour les équations linéaires, dire que
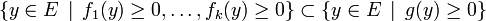
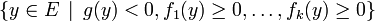
Lemme de Farkas, critère vectoriel d'inconsistance — Soient f1, ... , fk et h des formes linéaires sur un espace vectoriel réel E de dimension finie. Alors :
si et seulement si
- ( -h ) est une combinaison linéaire à coefficients positifs ou nuls de f1, ... , fk.
Par ce critère vectoriel d'inconsistance, on obtient facilement un critère d'inconsistance pour les systèmes affines directement apparenté, et d'aspect un peu plus simple :
Lemme de Farkas, critère affine d'inconsistance — Soient f1, ... , fk des formes affines sur un espace affine réel E de dimension finie. Alors :
si et seulement si
- (-1) est une combinaison linéaire à coefficients positifs ou nuls de f1, ... , fk.
On voit de nouveau là très nettement l'idée sous-jacente à tous ces énoncés, appliquée dans le cas de l'inconsistance : un système inconsistant implique (au sens du calcu propositionnel) l'inéquation absurde - 1 ≥ 0 ; le lemme de Farkas assure dès lors qu'elle peut en être déduite non seulement par des raisonnements plus ou moins compliqués mais aussi tout simplement par combinaisons des équations du système.
L'implication montante est évidente, montrons l'autre. On suppose donc
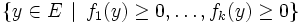
Introduisons un espace vectoriel Ê dans lequel E est un sous-espace affine de codimension 1 ne passant pas par l'origine. Toute forme affine sur E se prolonge d'une façon unique en une forme linéaire sur Ê. Notons
