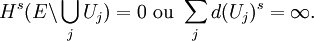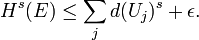Lemme de recouvrement de Vitali - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Théorème de recouvrement de Vitali
Définition. Pour un ensemble
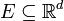
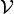
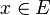
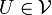
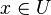
Théoreme. Soit
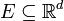
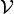
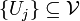
De plus, si E à une mesure de Hausdorff finie, alors pour tout ε > 0, on peut choisir cette sous-collection {Uj} telle que