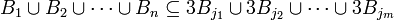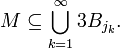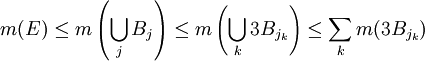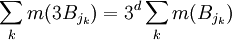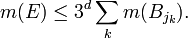Lemme de recouvrement de Vitali - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le lemme de recouvrement de Vitali est un résultat combinatoire de théorie de l'intégration des espaces euclidiens. Il est largement utilisé dans des démonstrations en analyse réelle.
L'idée basique du lemme est la suivante: supposons que l'on ait une collection de cercles dans le plan, autorisés à se superposer. Alors il est possible d'en extraire une sous-collection dont les cercles ne s'intersectent pas, et si l'on multiplie par 3 leurs rayons, ces cercles recouvrent la collection initiale.
Enoncé
- Version finie: Soit B1,...,Bn une collection de boules de
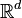
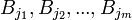
où
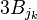
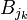
- Version infinie: Soit M un ensemble borné de
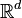
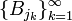
Applications
Une application directe du lemme de recouvrement de Vitali permet de prouver l'inégalité maximale de Hardy-Littlewood. Comme dans cette preuve, le lemme de Vitali est fréquemment utilisé lorsque, par exemple, on étudie la mesure de Lebesgue, m, d'un ensemble
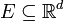
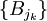
Comme on triple le rayon d'une boule de dimension d revient à multiplier son volume par un facteur de 3d, on a:
et donc:
On peut utiliser cette approche en considérant la dimension de Hausdorff à la place de la mesure de Lebesgue. Dans ce cas, on obtient le théorème suivant.
Preuve
- Dans la version finie :
Sans aucune perte de généralité et quitte à réordonner les indices des boules, on peut supposer qu'elles sont rangées par ordre de rayon décroissant, plus précisément si pour tout
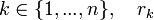
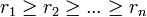
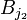
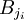
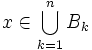
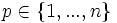
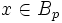
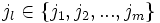
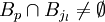
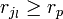
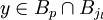
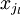
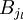
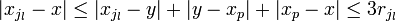
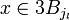
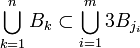
- Dans la version infinie :
On peut supposer sans perte de généralité que la famille des rayons est bornée. Sinon, comme le domaine est borné, une seule boule suffisamment grosse suffit à couvrir M. On reproduit la preuve précédente en prendant à chaque fois une boule dont le rayon excède la moitié de la borne supérieure des boules qui n'intersectent pas la zone déjà couverte. Eventuellement, le procédé peut s'arrêter en temps fini si on a tout recouvert. Soit B(x,r) une boule de la collection initiale. Si la séquence s'est arrêtée, il est clair qu'elle intersecte une des boules choisies, sinon on aurait pu continuer la séquence. Sinon, la suite des rayons tend vers 0 car on ne peut loger une infinité de boules disjointes de rayon minoré dans un domaine borné. Alors la boule B(x,r) intersecte la suite des rayons des boules dès que cette séquence passe en dessous de r. Finalement, dans tout les cas, toute boule B(x,r) de la famille intersecte une boule de rayon plus grand de la sous-famille extraite. Cela donne le résultat par l'inégalité triangulaire comme précédemment.