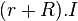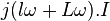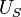Ligne à haute tension - Définition

Caractéristiques électriques

Puissances transportées

Des lignes à haute tension à Lund en Suède

Pertes de puissance

Malgré l'effort entrepris pour limiter la résistance, le transport de l'électricité engendre des pertes d’énergie importantes, principalement par effet Joule. À titre d'exemple, pour le réseau de transport d'électricité en France, ces pertes sont estimées en moyenne à 2,5 % de la consommation globale, soit 11,5 TWh par an ().

Pour ne pas subir de pertes importantes, on utilise donc deux techniques :

• augmenter le nombre de conducteurs : certaines lignes comportent pour chacune des phases jusqu’à quatre câbles distants de quelques centimètres ;
• diminuer l'intensité du courant en élevant la tension : pour une puissance transportée identique, si on augmente la tension, l'intensité du courant électrique diminue et les pertes dues au passage du courant dans le fil seront réduites selon le carré de l'intensité.

Toutefois, la tension servie aux particuliers doit rester inchangée (230 V en France ou 120 V au Québec pour les installations domestiques) et dans le domaine de la basse tension afin de limiter les risques pour les utilisateurs. Il faut donc l'abaisser au plus près de ceux-ci. Comme on ne sait pas le faire de façon simple avec le courant continu (cf. HVDC), on a recours au courant alternatif (de fréquence 50 Hz en France ou 60 Hz au Québec et Amérique du Nord) et à des transformateurs.

Il faut également prendre en compte le risque d'arc électrique entre deux conducteurs. Ce risque est d'autant plus important que la tension est élevée. Cela impose des contraintes d'isolement plus fortes et nécessite notamment :

• pour les lignes aériennes, d'écarter suffisamment les conducteurs, (typiquement 1 cm/kV), ce qui a pour conséquence d'augmenter proportionnellement la dimension des matériels associés (isolateurs, pylônes…) ;
• pour les câbles (enterrés ou non), d'augmenter les épaisseurs d'isolants, d'ajouter des écrans de masse, voire de recourir à des technologies différentes (par exemple câbles à isolation gazeuse).

Intensité du courant

L'intensité maximale du courant transportable dans une ligne est liée à la résistance de ses conducteurs, et donc à leur section et à la résistivité des matériaux les constituant.

Un courant circulant dans les conducteurs va créer des pertes, et donc une élévation de température. Un équilibre thermique va s'établir entre les pertes dans le conducteur, et l'énergie transmise par le conducteur à son milieu ambiant (l'air) par convection et rayonnement. Les gestionnaires du réseau devront limiter le courant et donc la température du conducteur à un niveau acceptable : la déformation due à la chaleur doit respecter la limite d'élasticité des cables, et la flèche de la ligne (son point bas par rapport au sol) doit rester suffisamment éloignée du sol pour ne pas mettre en danger les biens et personnes à proximité. La température limite admissible d'un conducteur aluminium est de l'ordre de 100 °C. A partir de là, le concepteur de la ligne définira en fonction de la température ambiante l'intensité maximale admissible. Des surcharges temporaires sont admissibles lorsque la température ambiante est suffisamment inférieure à la valeur maximale prise pour le dimensionnement.

Cependant le choix des sections de lignes doit se faire en fonction des courants maximaux à transporter, mais aussi en fonction de critères technico-économiques. Le choix d'une section plus importante entrainera une dépense plus importante, mais permettra de réduire les pertes. On peut même envisager de réaliser deux lignes transportant la moitié du courant, car les pertes de chaque ligne sont divisées par 4 — donc le total des pertes est divisé par 2. L’économie réalisée permet d’amortir la réalisation de la deuxième ligne. De plus, on conserve la possibilité de doubler l’intensité du courant en cas de besoin (opérations de maintenance, pannes sur l’autre ligne, …).

La densité du courant dans les lignes aériennes haute tension est d’environ 0,7 – 0,8 A/mm².

Chutes de tension

La problématique des chutes de tension sur une ligne à haute tension peut se se résumer ainsi : la tension étant fixe à une extrémité de la ligne,comment maintenir en bout de ligne une tension aussi constante que possible, et ceci quel que soit le courant traversant la ligne. Si le problème des chutes de tension existe aussi bien en basse tension, il peut être crucial sur les lignes à haute tension du fait de leur longueur. On verra également plus bas qu'à vide (en l'absence de courant), un phénomène paradoxal se produit sur les lignes à haute tension : la tension en extrémité de ligne est plus élevée qu'en entrée !

À vide

Si l'on considère le modèle en π lorsque le courant de sortie est nul, on remarque que le condensateur de sortie est alors en série (c'est-à-dire traversé par exactement la même intensité) avec la résistance et l'inductance de ligne.

On peut écrire : , soit :

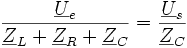
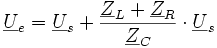
d'où l'on tire :

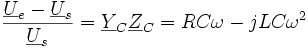
Pour une ligne aérienne, nous avons vu que , donc le deuxième terme est prédominant, ce qui conduit à une tension de sortie supérieure de quelques pour cent à la tension d'entrée. Ce phénomène est appelé effet Ferranti.

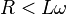
En charge

La f.é.m d'un alternateur est constante et égale à la somme vectorielle de la résistance interne fois le courant qui la traverse plus l'impédance interne fois le même courant plus la somme (résistance et impédance) de la ligne fois le courant plus la tension au bornes de la charge qui est en parallèle avec la capacité de la ligne.

Puisque la ligne en charge présente un aspect inductif, alors la formule sera:

, soit :

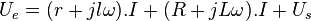
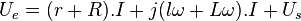
Si l'intensité appelée I augmente les deux termes et augmentent donc diminue à l’extrémité de la ligne. Pour y remédier, il y a deux possibilités : soit demander aux groupes de fournir plus de réactif soit insérer les batteries de condensateurs dans le réseau ou bien les deux solutions à la fois. L'ajout de la batterie de condensateur diminue le vecteur jlw inductif puisqu'elle impose un vecteur capacitif -j/cw opposé au vecteur inductif ce qui augmente le vecteur Us.