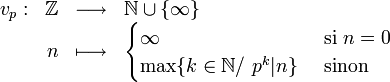Valuation - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, plus particulièrement en géométrie algébrique et en théorie des nombres, une valuation, ou valuation de Krull, est une mesure de la multiplicité. La notion est une généralisation de la notion de degré ou d'ordre d'annulation d'un polynôme formel en algèbre, du degré de divisibilité par un nombre premier en théorie des nombres, de l'ordre d'un pôle en analyse complexe ou du nombre de points de contact entre deux variétés algébriques en géométrie algébrique.
Définition
On appelle valuation une application d'un anneau commutatif unitaire
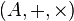
qui vérifie les propriétés suivantes :
-
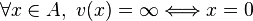
-
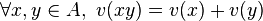
-
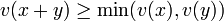
Notes :
- On utilise les conventions classiques
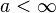
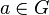
- Certains auteurs se restreignent à une valuation sur un corps.
- Lorsque A est un corps, la deuxième propriété se traduit par : v est un morphisme de (A*,x) dans (G,+), si bien que v(A*) est un sous-groupe de G.
- Lorsque A est un corps, on demande parfois à v d'être surjective, mais on peut toujours se ramener à cette situation en remplaçant G par v(A*).
Valuations discrètes
Lorsque
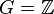
ou
Les classes d'équivalence des valuations discrètes sur un anneau A sont appelées places.
Valuation triviale
La valuation
est dite valuation triviale.
Exemples
Les applications suivantes sont des valuations.
Ordre d'annulation d'un polynôme
Soit K un corps (commutatif) et K[X] l'anneau des polynômes à coefficients dans K. Pour
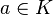
qui à un polynôme P non nul associe l'ordre de multiplicité de la racine a dans P (ordre qui vaut 0 si a n'est pas racine, et l'infini si P est nul).
Si P est non nul, va(P) est égal au degré du plus petit monôme non nul de P(a + X).
Note : Si a appartient à une extension L de K (par exemple à la clôture algébrique de K), la valuation va sur L[X] se restreint en une valuation sur K[X].
Ordre d'annulation d'une fraction rationnelle
Soit K un corps et K(X) le corps des fractions rationnelles à coefficients dans K. Soit
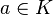
qui à une fraction rationnelle associe la différences des ordres d'annulation du numérateur et du dénominateur en a. Si v(R) est positif, il s'agit de l'ordre d'annulation de R en a, si v(R) est strictement négatif, il s'agit de l'ordre du pôle de R en a.
Opposé du degré d'un polynôme
Soit K un corps et K[X] l'anneau des polynômes à coefficients dans K. On définit l'application
qui à un polynôme P associe l'opposé de son degré avec la convention
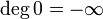
Ordre d'une série de Laurent
- Sur le corps F((T)) des séries formelles de Laurent sur un corps commutatif F, on a une valuation en associant à tout série de Laurent son ordre en un élément donné de F.
Ordre d'une fonction méromorphe
- Si U est un ouvert connexe non vide du corps des nombres complexes et si a est un point de U, on a une valuation sur le corps des fonctions méromorphes sur U en associant à tout fonction méromorphe son ordre au point a'.
Valuation p-adique
Pour p un nombre premier, on définit l'application
qui à un entier n associe l'exposant de p dans la décompositon en nombres premiers de n, avec la convention
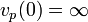
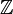


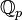
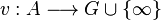
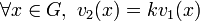
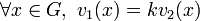
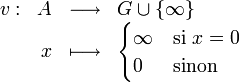
![\begin{array}{rrcl} v_a: & K[X]& \longrightarrow & \Z \cup \{\infty\} \\ & P & \longmapsto & \sup\left\{k\in \N/\ \exists R \in K[X],\ P(X)=(X-a)^kR(X)\right\}\end{array}](https://static.techno-science.net/illustration/Definitions/autres/2/20ac316826d502d2622898c0f13c94b7_80d3caec3a30a376107527e945ac81bc.png)
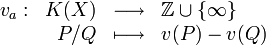
![\begin{array}{rrcl} v_\infty: & K[X] & \longrightarrow & \Z \cup \{\infty\} \\ & P & \longmapsto & -\deg P\end{array}](https://static.techno-science.net/illustration/Definitions/autres/5/59a92171a81a747685aca773cc21d6d7_dc4741d49d8313f23be55070220ff64a.png)