Locality sensitive hashing - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Locality Sensitive Hashing (LSH) est une méthode de recherche approximative dans des espaces de grande dimension. C'est une solution au problème de la malédiction de la dimension qui apparait lors d'une recherche des plus proches voisins en grande dimension. L'idée principale est d'utiliser une famille de fonction de hachage choisies telles que des points proches dans l'espace d'origine aient une forte probabilité d'avoir la même valeur de hachage. La méthode a de nombreuses applications en vision artificielle, traitement automatique de la langue, bio-informatique...
Définition
Une famille LSH

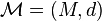

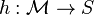
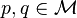

- si
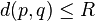
![Pr_{h \in H} [h(p) = h(q)] \ge P_1](https://static.techno-science.net/illustration/Definitions/autres/e/e48dbc8481e2df39bde5987c0de2a8f7_f9d2a5b91e3924bf0a6fb05844a2373e.png)
- si
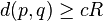
![Pr_{h \in H} [h(p) = h(q)] \le P_2](https://static.techno-science.net/illustration/Definitions/autres/f/f00ebad58eb9407f4281061cdcd646be_b972f003e7d334c63fc89c103b26ce4d.png)
Par construction, les fonctions de hachage doivent permettre aux points proches d'entrer fréquemment en collision (i.e. h(p) = h(q)) et inversement, les points éloignés ne doivent entrer que rarement en collision. Pour que la famille LSH soit intéressante, il faut donc P1 > P2. La famille

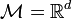
Une définition alternative est définie par rapport à un univers U possédant une fonction de simlarité
![\phi : U \times U \to [0,1]](https://static.techno-science.net/illustration/Definitions/autres/3/33b14ac9cf67f9c2f70bcfe923baac13_c538bd4c881dfe0dc2abf0289d530ba7.png)
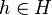
![Pr_{h \in H} [h(a) = h(b)] = \phi(a,b)](https://static.techno-science.net/illustration/Definitions/autres/e/ebbc28ce3e44e528fbdc537a6806c382_a4104c5f91556cfc2698109735273644.png)
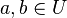
Méthodes
Échantillonnage par bit pour la distance de Hamming
Une façon simple de construire une famille LSH est par échantillonnage de bit. Cette approche est adaptée à la distance de Hamming dans un espace binaire de dimension d, i.e. un point de l'espace appartient à {0,1}d. La famille

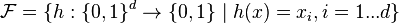
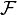
Cette famille possède les paramètres suivants :
- P1 = 1 − R / d
- P2 = 1 − cR / d.
Applications
LSH a été appliqué dans plusieurs domaines, en particulier pour la recherche d'image par le contenu, la comparaison de sequence d'ADN, la recherche par similarité de documents audios.
L'algorithme LSH pour la recherche par plus proche voisins
L'application principale de LSH est de fournir un algorithme efficace de recherche des plus proches voisins.
L'algorithme donne une méthode de construction d'une famille LSH
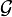
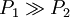

- Pré-traitement
En pré-traitement, l'algorithme définit donc une nouvelle famille
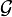

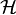
L'algorithme construit ensuite L tables de hachage, correspondant chacune à une fonction de hachage g. La je table de hachage contient alors les points de
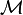
- Recherche d'un point requête q
Pour un point requête q, l'algorithme itère sur les L fonctions de hachage g. Pour chaque g considérée, on trouve les points hachés à la même position que le point requête q dans la table correspondante. Le processus s'arrête dès qu'un point r est trouvé tel que
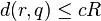
Étant donné les paramètres k et L, l'algorithme a les garanties de performance suivantes :
- temps de pré-traitement : O(nLkt), où t est le temps d'évaluation d'une fonction
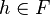
- mémoire : O(nL)
- temps de requête :
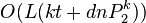
- l'algorithme a une probabilité de trouver un point à une distance cR de la requête q (si un tel point existe) avec une probabilité