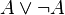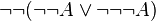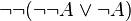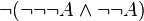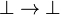Logique minimale - Définition

Logique minimale et logique classique

La traduction de Gödel

La logique minimale, amputée du traitement de la négation, semble bien pauvre devant la logique classique ou la logique intuitionniste. Elle n'en est cependant pas si éloignée. On montre en effet, que, pour toute formule A, il existe une formule A', équivalente à A en logique classique, telle que A est prouvable en logique classique si et seulement si A' est prouvable en logique minimale. A' est obtenue au moyen de la traduction de Gödel, définie itérativement comme suit :

pour toute formule atomique différente de

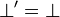
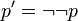
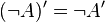
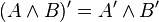
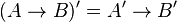
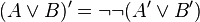
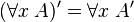
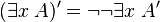
Autrement dit, la traduction de Gödel d'une formule consiste à rajouter des doubles négations devant les formules atomiques, les disjonctions et les quantificateurs existentiels. Cela signifie qu'en logique classique, il suffit de faire appel à des raisonnements par l'absurde seulement devant des formules atomiques, des disjonctions ou des quantificateurs existentiels.

Exemples

Par exemple, le tiers exclu est un théorème de la logique classique, mais pas de la logique minimale. Par contre, en logique minimale la formule est valide. En effet, celle-ci est équivalente, en logique minimale, à ou à ou encore à , c'est-à-dire à qui est une formule valide.