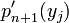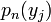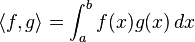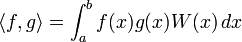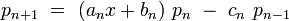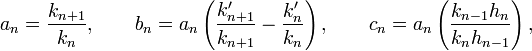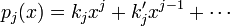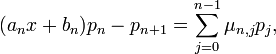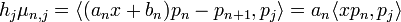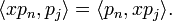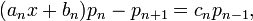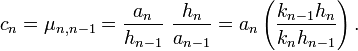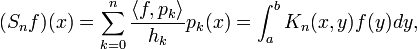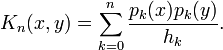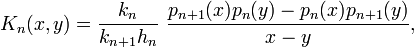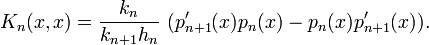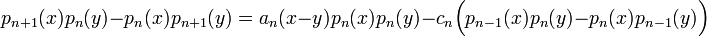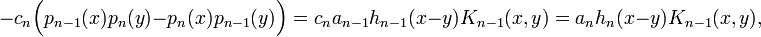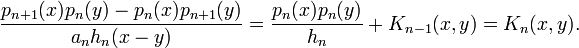Polynômes orthogonaux - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, une suite de polynômes orthogonaux est une suite infinie de polynômes p0(x), p1(x), p2(x) ... à coefficients réels, dans laquelle chaque pn(x) est de degré n, et telle que les polynômes de la suite sont orthogonaux deux à deux pour un produit scalaire de fonctions donné.
Introduction
Le produit scalaire de fonctions le plus simple est l'intégrale du produit de ces fonctions, sur un intervalle borné :
Plus généralement, on peut introduire une "fonction poids" W(x) dans l'intégrale (sur l'intervalle d'intégration ]a,b[, W doit être à valeurs finies et strictement positives, et l'intégrale du produit de la fonction poids par un polynôme doit être finie ; les bornes a,b peuvent être infinies) :
Avec cette définition du produit scalaire, deux fonctions sont orthogonales entre elles si leur produit scalaire est égal à zéro (de la même manière que deux vecteurs sont orthogonaux (perpendiculaires) si leur produit scalaire égale zéro). On introduit alors la norme associée :
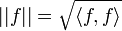
L'intervalle d'intégration est appelé intervalle d'orthogonalité.
Le domaine des polynômes orthogonaux a été développé durant le XIXème siècle par Stieltjes, comme outil de la théorie analytique des fractions continues. De multiples applications en ont découlé, en mathématiques et en physique.
Propriétés
Toute suite de polynômes
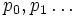
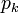
![\R[x]](https://static.techno-science.net/illustration/Definitions/autres/5/52d4d6c0345834ef4ae2c597d02209d5_b84be2545494e2d7045733dc7cfee6c9.png)
![(\mathbb{R}_n[x])_{n\in\N}](https://static.techno-science.net/illustration/Definitions/autres/b/b4d071de231b5d7278ba905361e0c9ff_9d3d38ccf5acd48823c3f75e983023de.png)
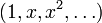
Quand on construit une base orthogonale, on peut être tenté de la rendre orthonormale, c'est-à-dire telle que
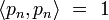
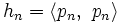
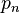
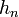
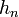
-
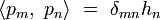
où δmnhn est le delta de Kronecker.
Toute suite (pk) de polynômes orthogonaux possède un grand nombre de propriétés remarquables. Pour commencer :
Lemme 1 :
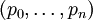
![\R_n[x]](https://static.techno-science.net/illustration/Definitions/autres/f/f462241d6c1efbdc3c7cbc1297ab3cdf_b424dd7ce039b09095a30c6b95dbb582.png)
Lemme 2 : pn est orthogonal à
![\R_{n-1}[x]](https://static.techno-science.net/illustration/Definitions/autres/4/4255a1da00b2bfe966fff3d993254522_def365e31957e63a9c5bb5a5c19f0dd9.png)
Le lemme 1 est dû au fait que pk est de degré k. Le lemme 2 vient de ce que, de plus, les pk sont orthogonaux deux à deux.
Relation de récurrence
Pour toute suite de polynômes orthogonaux, il existe une relation de récurrence relativement à trois polynômes consécutifs.
Les coefficients an,bn,cn sont donnés par
où kj et kj' désignent les deux premiers coefficients de pj :
et hj le produit scalaire de pj par lui-même :
-
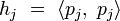
(Par convention,
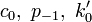
Avec les valeurs données pour an et bn, le polynôme (anx + bn)pn − pn + 1 est de degré <n (les termes de degrés n+1 et n s'éliminent). On peut donc l'exprimer sous forme d'une combinaison linéaire des éléments de la base
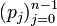
![\R_{n-1}[x]](https://static.techno-science.net/illustration/Definitions/autres/4/4255a1da00b2bfe966fff3d993254522_def365e31957e63a9c5bb5a5c19f0dd9.png)
avec
(car pour j<n, pj est orthogonal à pn et pn+1).
De plus, de par la forme intégrale du produit scalaire,
Pour j<n-1, ce produit scalaire est nul car xpj est de degré <n.
Pour j=n-1, il est égal à
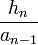
On peut conclure :
avec
Noyau de Christoffel-Darboux
Dans l'espace L2 associé à W, notons Sn la projection orthogonale sur
![\R_n[x]](https://static.techno-science.net/illustration/Definitions/autres/f/f462241d6c1efbdc3c7cbc1297ab3cdf_b424dd7ce039b09095a30c6b95dbb582.png)
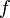
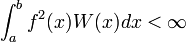
où Kn est le noyau de Christoffel-Darboux, défini par :
La relation de récurrence précédente permet alors de montrer :
Existence de racines réelles
Tout polynôme d'une suite de polynômes orthogonaux dont le degré n est supérieur ou égal à 1 admet n racines distinctes, toutes réelles, et situées strictement à l'intérieur de l'intervalle d'intégration (c'est une propriété remarquable : il est rare, pour un polynôme de degré élevé dont les coefficients ont été choisis au hasard, d'avoir toutes ses racines réelles)
Soit m le nombre des points où pn change de signe à l'intérieur de l'intervalle d'orthogonalité ; notons
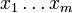
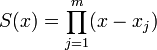
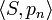
Position des racines
Les racines des polynômes se trouvent strictement entre les racines du polynôme de degré supérieur dans la suite.
On met d'abord tous les polynômes sous une forme standardisée telle que le coefficient dominant soit positif (ce qui ne change pas les racines), puis on effectue une récurrence sur n. Pour n=0 il n'y a rien à démontrer. Supposons la propriété acquise jusqu'au rang n. Notons
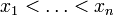
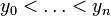
 et
et  . Ceci permet de conclure :
. Ceci permet de conclure :
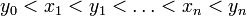
Une autre méthode de démonstration est de prouver (par récurrence, ou plus simplement en utilisant le noyau de Christoffel-Darboux) que pour tout n et tout x,  , pour en déduire que
, pour en déduire que