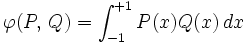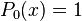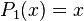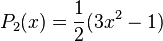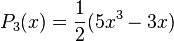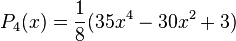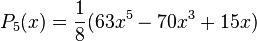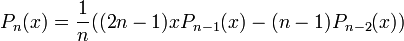Polynôme de Legendre - Définition
Les polynômes de Legendre sont des solutions y de l'équation différentielle de Legendre :
![\frac{d}{dx}\left[(1-x^{2})\frac{dy}{dx}\right]+l(l+1)y=0](https://static.techno-science.net/illustration/Definitions/autres/9/94e557315ace549c4010e73f5a45b133_b3a4c42d23142f2ff9600d68b365e8cb.png)
où l est un entier naturel représentant l'ordre du polynôme.
On peut aussi les définir par l'intégrale de contour :
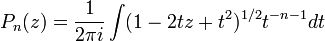
où le contour entoure l'origine et est pris dans le sens des aiguilles d'une montre.
Les premiers polynômes sont :
La relation de récurrence entre les différents polynomes s'écrit:
Ces polynômes sont orthogonaux par rapport au produit scalaire

![\R[X]](https://static.techno-science.net/illustration/Definitions/autres/6/60ed190117e7614d227f8d1693161a5b_67a4b8800a94a9a175a1ac6f97f6cf7d.png)
-