Métaheuristique - Définition

Applications

Les métaheuristiques sont souvent employées pour leur facilité de programmation et de manipulation. Elles sont en effet facilement adaptables à tout type de problème d’optimisation. Toutefois, elles sont le plus judicieusement employées sur des problèmes d’optimisation difficile, où des méthodes d’optimisation plus classiques (méthodes déterministes, notamment) montrent leurs limites.

De façon générale, on peut considérer que des problèmes présentant les caractéristiques suivantes sont assez propices à l’utilisation de métaheuristiques :

• NP-complétude,
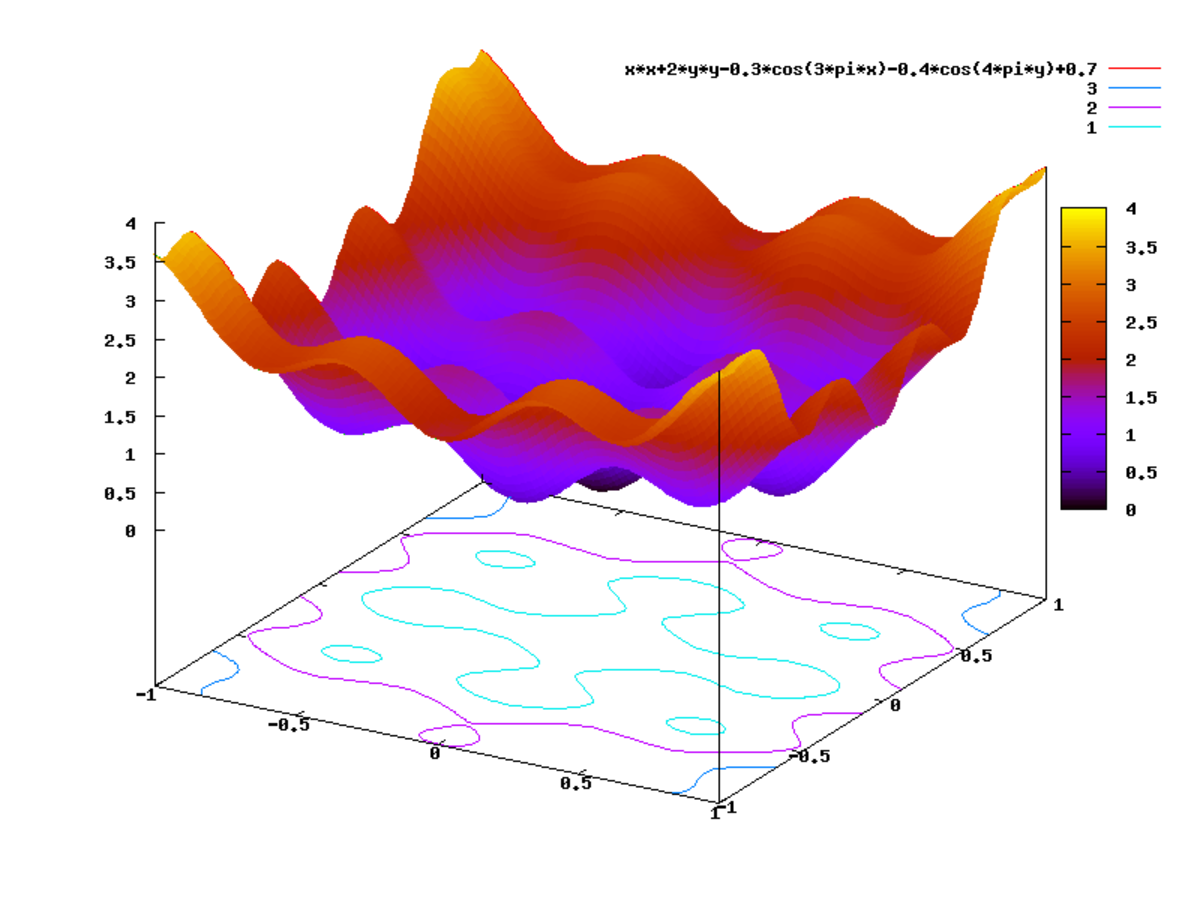
• nombreux optima locaux,
• discontinuités,
• contraintes fortes,
• non dérivabilité,
• temps de calcul de la fonction objectif prohibitif,
• solution approchée souhaitée,
• etc.

Tests

Exemple de problème test à minimiser (présenté ici pour deux variables)

Pour tester une métaheuristique, une première étape consiste à utiliser des fonctions mathématiques spécialement conçues. Les algorithmes sont évalués sur la base d’un ensemble de fonctions, plus ou moins difficiles, puis comparés entre eux.

Les métaheuristiques étant généralement stochastiques, les tests doivent en principe être répétés un grand nombre de fois, puis exploités via des méthodes statistiques. Cependant, cette pratique reste relativement peu répandue dans la littérature spécialisée.

Problèmes réels

Dans un numéro spécial de la revue scientifique European Journal of Operational Research, consacré aux applications des métaheuristiques, les éditeurs ont constatés que la majorité des 20 articles publiés le furent dans deux domaines : les problèmes d'ordonnancement et de logistique. Les méthodes les plus utilisés appartiennent à la famille des algorithmes évolutionnaires, souvent hybridés avec des méthodes de recherche locale.

Quelques exemples de problèmes concrets, optimisés via des métaheuristiques :

• problèmes de tournée de véhicules,
• optimisation de réseaux mobiles UMTS,
• gestion du trafic aérien,
• optimisation des plans de chargement des cœurs de réacteurs nucléaires,
• etc.

Avantages et inconvénients

Les métaheuristiques étant très généralistes, elles peuvent être adaptées à tout type de problème d’optimisation pouvant se réduire à une « boîte noire ». Elles sont souvent moins puissantes que des méthodes exactes sur certains types de problèmes. Elles ne garantissent pas non plus la découverte de l’optimum global en un temps fini. Cependant, un grand nombre de problèmes réels n’est pas optimisable efficacement par des approches purement mathématiques, les métaheuristiques peuvent alors être utilisées avec profit.

La notion d’efficacité se rapporte généralement à deux objectifs contradictoires : la vitesse et la précision. La vitesse est souvent mesurée en nombre d’évaluations de la fonction objectif, qui est la plupart du temps la partie la plus gourmande en temps de calcul. La précision se rapporte à la distance entre l’optimum trouvé par la métaheuristique et l’optimum réel, soit du point de vue de la solution, soit de celui de la valeur. Bien souvent, un algorithme rapide est peu précis, et inversement.

Généralement, un choix doit être fait quant au critère d’arrêt adéquat. Un nombre d’évaluation ou un temps imparti est souvent utilisé, mais on peut également choisir d’atteindre une valeur donnée de la fonction objectif (le but étant alors de trouver une solution associée). Il est également possible de choisir des critères dépendants du comportement de l’algorithme, comme une dispersion minimale de la population de points ou un paramètre interne approprié. En tout état de cause, le choix du critère d’arrêt influencera la qualité de l’optimisation.

Le théorème du « no free lunch » explique qu’aucune instance de métaheuristique ne peut prétendre être la meilleure sur tous les problèmes. Une métaheuristique (M) n’est performante que pour une classe de problème (P) donnée.

L’utilisation de métaheuristiques peut paraître relativement simple, en première approche, mais il est souvent nécessaire d’adapter l’algorithme au problème optimisé. Tout d’abord, principalement dans le cadre de l’optimisation combinatoire, le choix de la représentation des solutions manipulées peut être crucial. Ensuite, la plupart des métaheuristiques disposent de paramètres dont le réglage n’est pas nécessairement trivial. Enfin, obtenir de bonnes performances passe généralement par une étape d’adaptation des diverses étapes de l’algorithme (initialisation, notamment). En pratique, seul le savoir-faire et l’expérience de l’utilisateur permet de gérer ces problèmes.

Il est admis que, d’un point de vue très général, aucune métaheuristique n’est réellement meilleure qu’une autre. En effet, une métaheuristique ne peut prétendre être plus efficace sur tous les problèmes, bien que certaines instances (c’est-à-dire l’algorithme lui même, mais aussi un choix de paramètres et une implémentation donnée) puissent être plus adaptées que d’autres sur certaines classes de problèmes. Cette constatation est décrite par le théorème du no free lunch (« pas de dîner gratuit »).

En dernière analyse, il est parfois possible que le choix de la représentation des solutions, ou plus généralement des méthodes associées à la métaheuristique, ait plus d’influence sur les performances que le type d’algorithme lui-même. En pratique, cependant, les métaheuristiques se montrent plus puissantes que les méthodes de parcours exhaustif ou de recherche purement aléatoire.