Métaheuristique - Définition

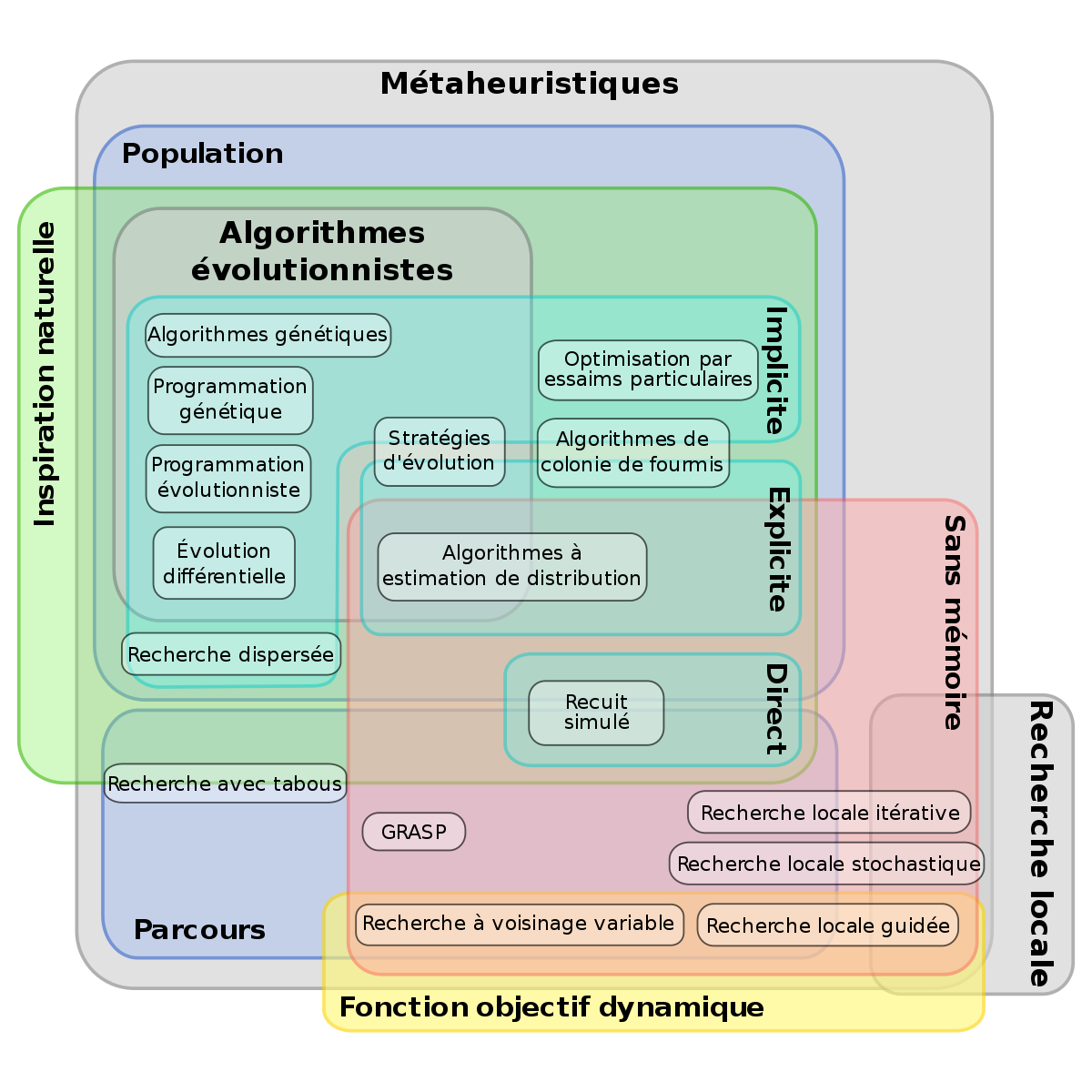
Classification

Les métaheuristiques peuvent être classées de nombreuses façons. Ce diagramme tente de présenter où se placent quelque unes des méthodes les plus connues. Un élément présenté à cheval sur différentes catégories indique que l'algorithme peut être placé dans l'une ou l'autre classe, selon le point de vue adopté.

Parcours et population

Principe général des métaheuristiques (a) à population, et (b) à parcours.

Les métaheuristiques les plus classiques sont celles fondées sur la notion de parcours. Dans cette optique, l’algorithme fait évoluer une seule solution sur l’espace de recherche à chaque itération. La notion de voisinage est alors primordiale.

Les plus connues dans cette classe sont le recuit simulé, la recherche avec tabous, la recherche à voisinage variable, la méthode GRASP ou encore les méthode de bruitage.

Dans cette classification, l’autre approche utilise la notion de population. La métaheuristique manipule un ensemble de solutions en parallèle, à chaque itération.

On peut citer les algorithmes génétiques, l’optimisation par essaims particulaires, les algorithmes de colonies de fourmis.

La frontière est parfois floue entre ces deux classes. On peut ainsi considérer qu’un recuit simulé où la température baisse par paliers, a une structure à population. En effet, dans ce cas on manipule un ensemble de points à chaque palier, il s’agit simplement d’une méthode d’échantillonnage particulière.

Emploi de mémoire

Les métaheuristiques utilisent l’historique de leur recherche pour guider l’optimisation aux itérations suivantes.

Dans le cas le plus simple, elles se limitent à considérer l’état de la recherche à une itération donnée pour déterminer la prochaine itération : il s’agit alors d’un processus de décision markovien, et on parlera de méthode sans mémoire. C’est le cas de la plupart des méthodes de recherche locale.

Beaucoup de métaheuristiques utilisent une mémoire plus évoluée, que ce soit sur le court terme (solutions visitées récemment, par exemple) ou sur le long terme (mémorisation d’un ensemble de paramètres synthétiques décrivant la recherche).

Fonction objectif statique ou dynamique

La plupart des métaheuristiques utilisent la fonction objectif en l’état, et font évoluer leur comportement de recherche de l’optimum. Cependant, certains algorithmes, comme la recherche locale guidée, modifient la représentation du problème, en incorporant l’information collectée durant la recherche, directement au sein de la fonction objectif.

Il est donc possible de classer les métaheuristiques selon qu’elles utilisent une fonction objectif statique (qui demeure inchangée tout au long de l’optimisation) ou dynamique (quand la fonction objectif est modifiée au cours de la recherche).

Nombre de structures de voisinage

La plupart des métaheuristiques utilisées dans le cadre des problèmes d’optimisation combinatoire utilisent une seule structure de voisinage. Cependant, des méthodes comme la recherche à voisinage variable permettent de changer de structure en cours de recherche.

Implicite, explicite, directe

Les métaheuristiques peuvent être qualifiées d’explicites (E, ici sur une somme de deux gaussiennes), d’implicites (I) ou de directes (D), selon la façon dont elles gèrent la transition entre deux itérations.

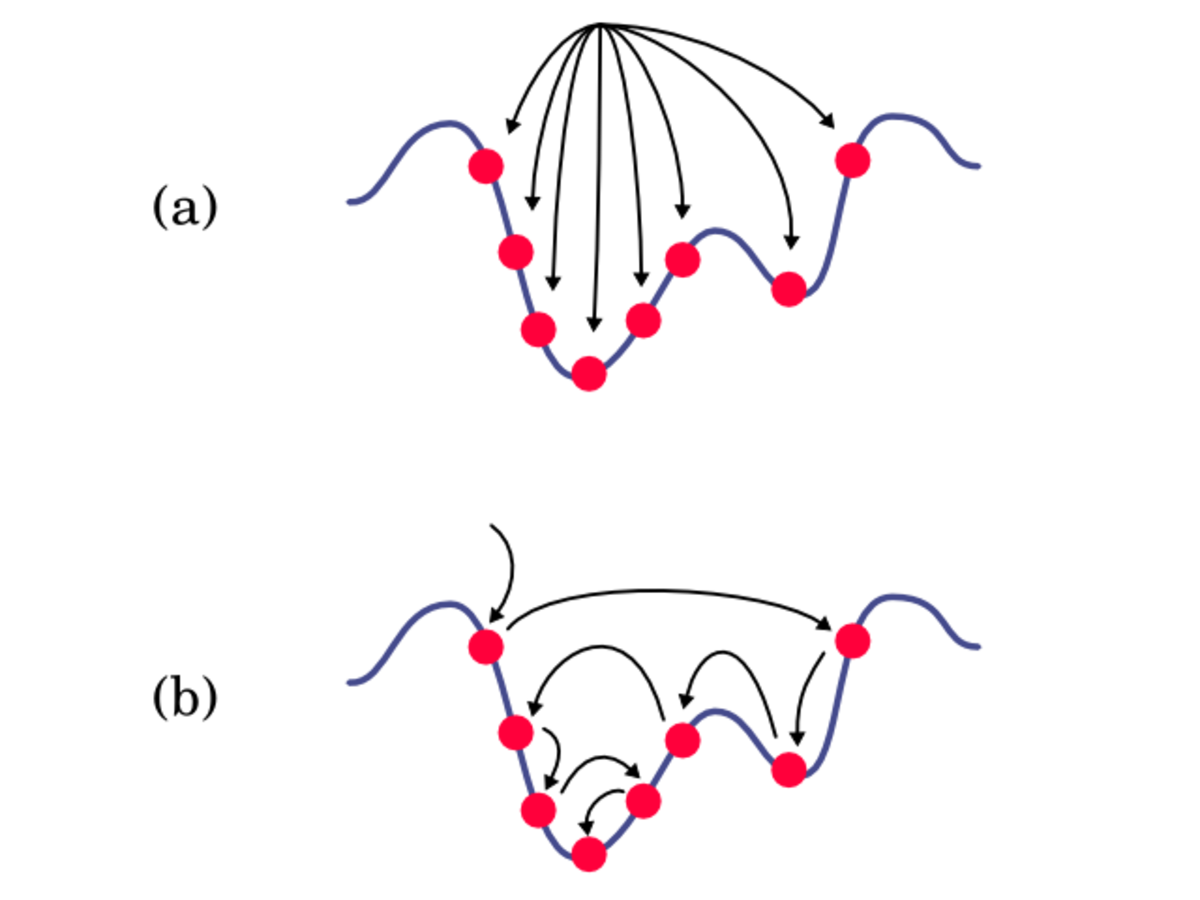
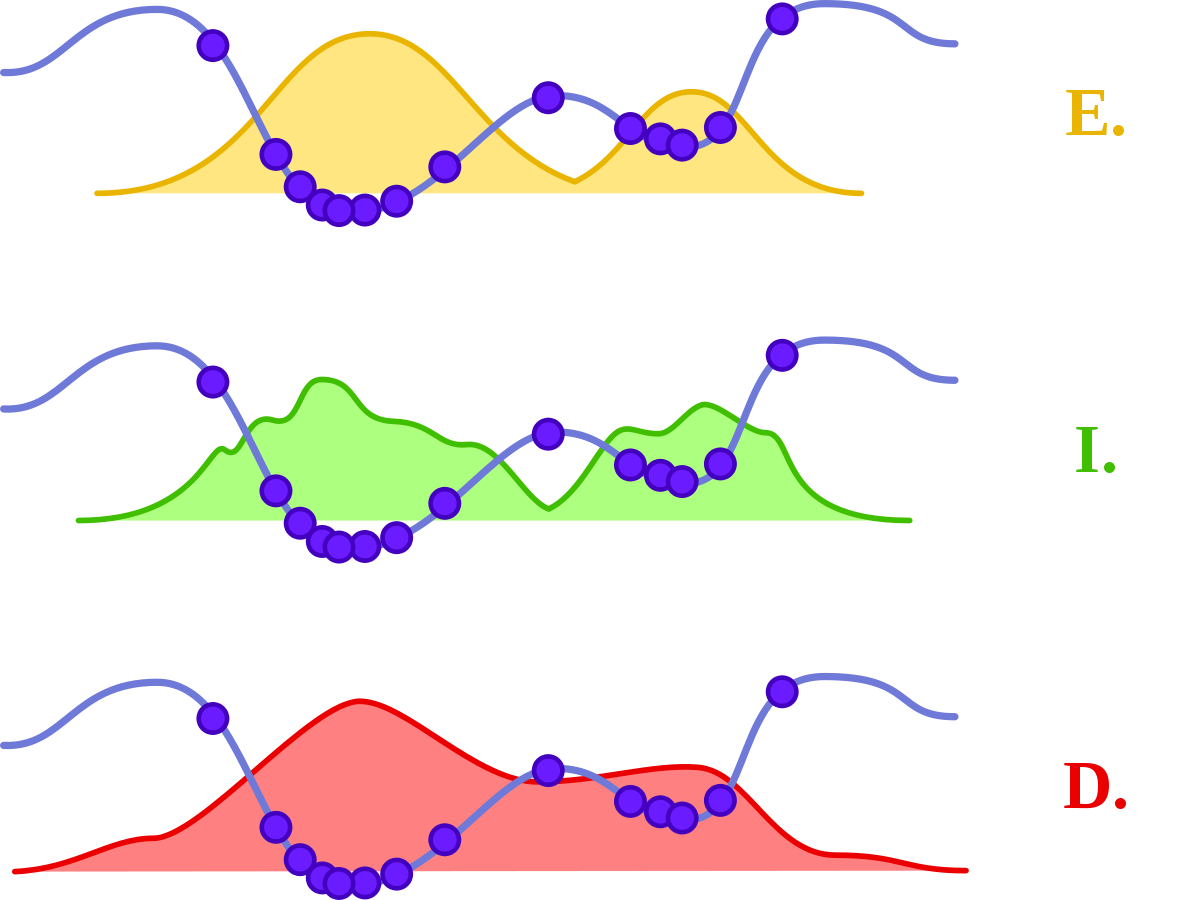
En considérant les métaheuristiques comme des méthodes itératives utilisant un échantillonnage de la fonction objectif comme base d’apprentissage (définition plus particulièrement adaptée aux métaheuristiques à populations) apparaît le problème du choix de l’échantillonnage.

Dans la très grande majorité des cas, cet échantillonnage se fait sur une base aléatoire, et peut donc être décrit via une distribution de probabilités. Il existe alors trois classes de métaheuristiques, selon l’approche utilisée pour manipuler cette distribution.

La première classe est celle des méthodes implicites, où la distribution de probabilité n’est pas connue a priori. C’est le cas par exemple des algorithmes génétiques, où le choix de l’échantillonnage entre deux itérations ne suit pas une loi donnée, mais est fonction de règles locales.

Par opposition, on peut donc classer les méthodes explicites, qui utilisent une distribution de probabilité choisie à chaque itération. C’est le cas des algorithmes à estimation de distribution.

Dans cette classification, le recuit simulé occupe une place particulière, puisqu’on peut considérer qu’il échantillonne la fonction objectif en utilisant directement celle-ci comme distribution de probabilité (les meilleures solutions ayant une probabilité plus grande d’être tirées). Il n’est donc ni explicite ni implicite, mais plutôt « direct ».

Évolutionnaire ou non

On trouve parfois une classification présentant les algorithmes d’optimisations stochastiques comme étant « évolutionnaires » (ou « évolutionnistes ») ou non. L’algorithme sera considéré comme faisant partie de la classe des algorithmes évolutionnaires s’il manipule une population via des opérateurs, selon un algorithme général donné.

Cette façon de présenter les métaheuristiques dispose d’une nomenclature adaptée : on parlera d’opérateurs pour toute action modifiant l’état d’une ou plusieurs solutions. Un opérateur construisant une nouvelle solution sera dénommé générateur, alors qu’un opérateur modifiant une solution existante sera appelé mutateur.

Dans cette optique, la structure générale des algorithmes évolutionnaires enchaîne des étapes de sélection, de reproduction (ou croisement), de mutation et enfin de remplacement. Chaque étape utilise des opérateurs plus ou moins spécifiques.

Taxinomie de l’hybridation

Taxinomie des métaheuristiques hybrides.

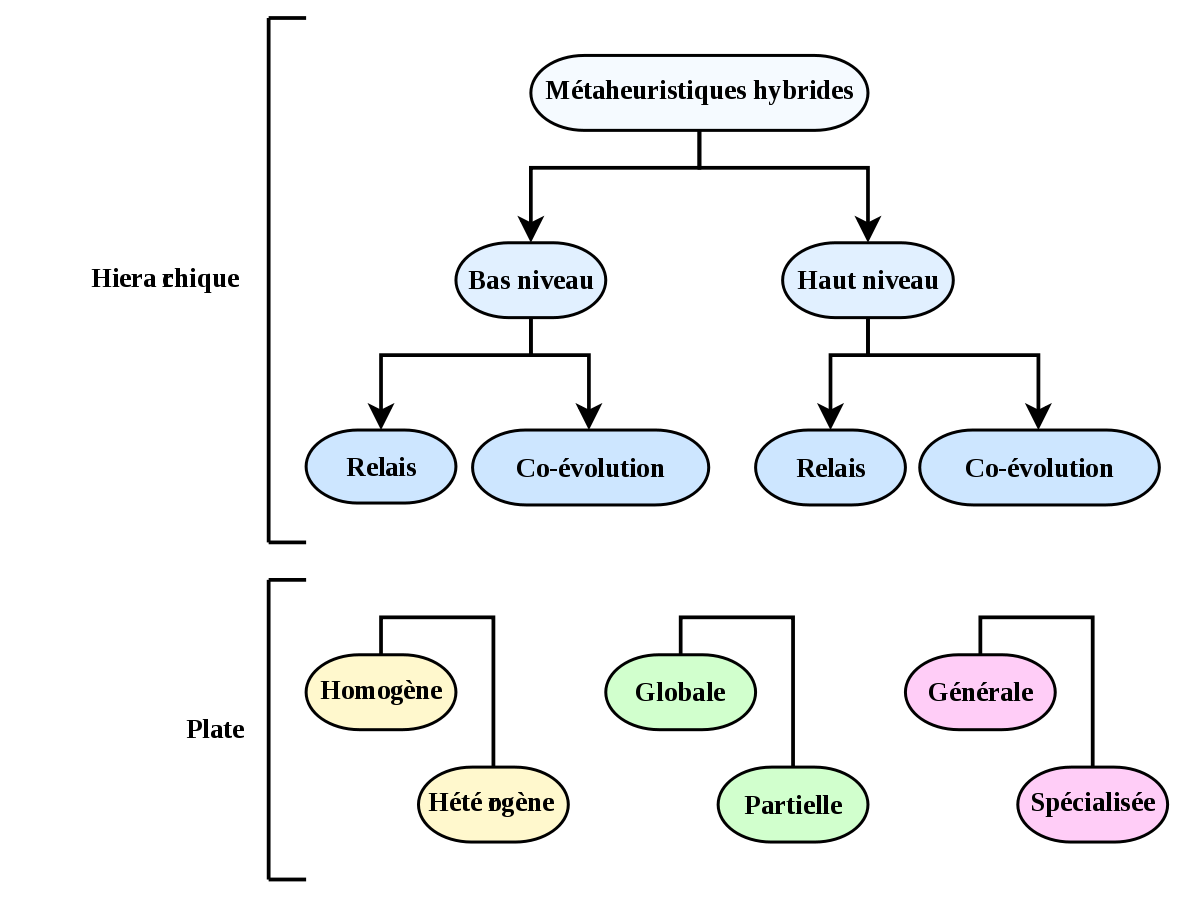
On parle d’hybridation quand la métaheuristique considérée est composée de plusieurs méthodes se répartissant les tâches de recherche. La taxinomie des métaheuristiques hybrides se sépare en deux parties : une classification hiérarchique et une classification plate. La classification est applicable aux méthodes déterministes aussi bien qu’aux métaheuristiques.

La classification hierarchique se fonde sur le niveau (bas ou haut) de l’hybridation et sur son application (en relais ou concurrente). Dans une hybridation de bas niveau, une fonction donnée d’une métaheuristique (par exemple, la mutation dans un algorithme évolutionnaire) est remplacée par une autre métaheuristique (par exemple une recherche avec tabou). Dans le cas du haut niveau, le fonctionnement interne « normal » des métaheuristiques n’est pas modifié. Dans une hybridation en relais, les métaheuristiques sont lancées les unes après les autres, chacune prenant en entrée la sortie produite par la précédente. Dans la concurrence (ou co-évolution), chaque algorithme utilise une série d’agents coopérants ensembles.

Cette première classification dégage quatre classes générales :

• bas niveau & relais (abrégé LRH en anglais),
• bas niveau & co-évolution (abrégé LCH),
• haut niveau & relais (HRH),
• haut niveau & co-évolution (HCH).

La seconde partie dégage plusieurs critères, pouvant caractériser les hybridations :

• si l’hybridation se fait entre plusieurs instances d’une même métaheuristique, elle est homogène, sinon, elle est hétérogène ;
• si les méthodes recherchent dans tout l’espace de recherche, on parlera d’hybridation globale, si elles se limitent à des sous-parties de l’espace, d’hybridation partielle ;
• si les algorithmes mis en jeu travaillent tous à résoudre le même problème, on parlera d’approche générale, s’ils sont lancés sur des problèmes différents, d’hybridation spécialisée.

Ces différentes catégories peuvent être combinées, la classification hierarchique étant la plus générale.