Métaheuristique - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Une métaheuristique est un algorithme d’optimisation visant à résoudre des problèmes d’optimisation difficile (souvent issus des domaines de la recherche opérationnelle, de l'ingénierie ou de l'intelligence artificielle) pour lesquels on ne connaît pas de méthode classique plus efficace.
Les métaheuristiques sont généralement des algorithmes stochastiques itératifs, qui progressent vers un optimum global, c'est-à-dire l'extremum global d'une fonction, par échantillonnage d’une fonction objectif. Elles se comportent comme des algorithmes de recherche, tentant d’apprendre les caractéristiques d’un problème afin d’en trouver une approximation de la meilleure solution (d'une manière proche des algorithmes d'approximation).
Il existe un grand nombre de métaheuristiques différentes, allant de la simple recherche locale à des algorithmes complexes de recherche globale. Ces méthodes utilisent cependant un haut niveau d’abstraction, leur permettant d’être adaptées à une large gamme de problèmes différents.
Généralités
Terminologies
On parle de méta, du grec « au-delà » (comprendre ici « à un plus haut niveau »), heuristique, du grec ευρισκειν / heuriskein, qui signifie « trouver ». En effet, ces algorithmes se veulent des méthodes génériques pouvant optimiser une large gamme de problèmes différents, sans nécessiter de changements profonds dans l’algorithme employé.
Une terminologie légèrement différente considère que les méta-heuristiques sont une forme d’algorithmes d’optimisation stochastique, hybridés avec une recherche locale. Le terme méta est donc pris au sens où les algorithmes peuvent regrouper plusieurs heuristiques. On rencontre cette définition essentiellement dans la littérature concernant les algorithmes évolutionnaires, où elle est utilisée pour désigner une spécialisation. Dans le cadre de la première terminologie, un algorithme évolutionnaire hybridé avec une recherche locale sera plutôt désigné sous le terme d’algorithme mémétique.
Les métaheuristiques sont souvent inspirées par des systèmes naturels, qu’ils soient pris en physique (cas du recuit simulé), en biologie de l’évolution (cas des algorithmes génétiques) ou encore en éthologie (cas des algorithmes de colonies de fourmis ou de l’optimisation par essaims particulaires).
Nomenclature
Le but d’une métaheuristique est de résoudre un problème d’optimisation donné : elle cherche un objet mathématique (une permutation, un vecteur, etc.) minimisant (ou maximisant) une fonction objectif, qui décrit la qualité d’une solution au problème.
L’ensemble des solutions possibles forme l’espace de recherche. L’espace de recherche est au minimum borné, mais peut être également limité par un ensemble de contraintes.
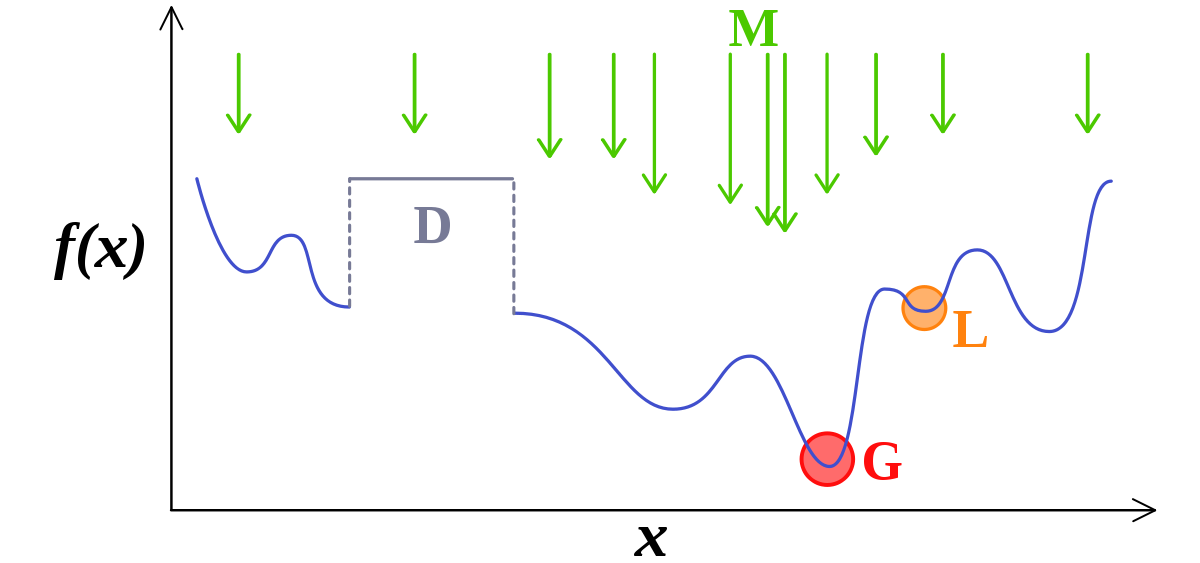
Les métaheuristiques manipulent une ou plusieurs solutions, à la recherche de l’optimum, la meilleure solution au problème. Les itérations successives doivent permettre de passer d’une solution de mauvaise qualité à la solution optimale. L’algorithme s’arrête après avoir atteint un critère d’arrêt, consistant généralement en l’atteinte du temps d’exécution imparti ou en une précision demandée.
Une solution ou un ensemble de solutions est parfois appelé un état, que la métaheuristique fait évoluer via des transitions ou des mouvements. Si une nouvelle solution est construite à partir d’une solution existante, elle est sa voisine. Le choix du voisinage et de la structure de donnée le représentant peut être crucial.
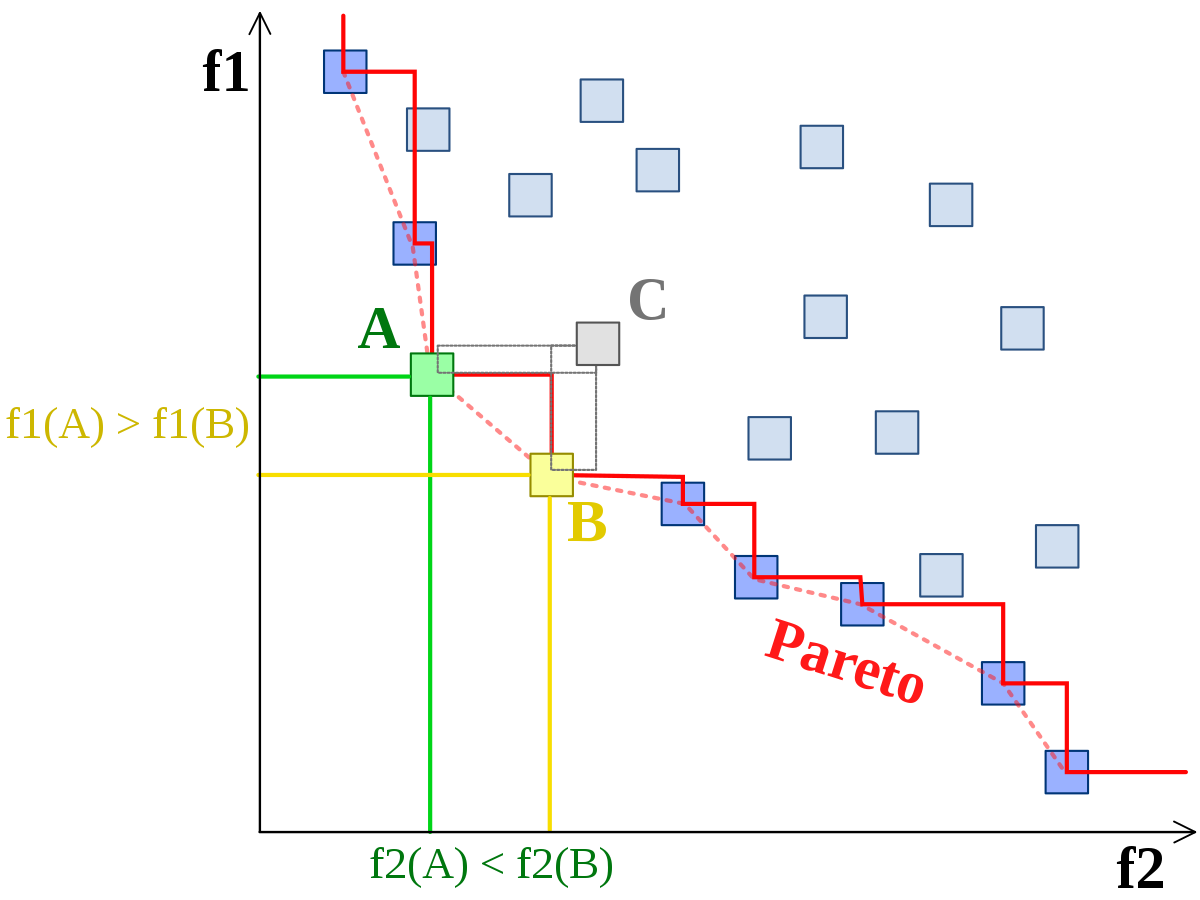
Lorsqu’une solution est associée à une seule valeur, on parle de problème mono-objectif, lorsqu’elle est associée à plusieurs valeurs, de problème multi-objectifs (ou multi-critères). Dans ce dernier cas, on recherche un ensemble de solutions non dominées (le « front de Pareto »), solutions parmi lesquelles on ne peut décider si une solution est meilleure qu’une autre, aucune n’étant systématiquement inférieure aux autres sur tous les objectifs.
Dans certains cas, le but recherché est explicitement de trouver un ensemble d’optimums « satisfaisants ». L’algorithme doit alors trouver l’ensemble des solutions de bonne qualité, sans nécessairement se limiter au seul optimum : on parle de méthodes multimodales.
Concepts généraux
Les métaheuristiques ne nécessitent pas de connaissances particulières sur le problème optimisé pour fonctionner, le fait de pouvoir associer une (ou plusieurs) valeurs à une solution est la seule information nécessaire.
En pratique, elles ne devraient être utilisées que sur des problèmes ne pouvant être optimisés par des méthodes mathématiques. Utilisées en lieu et place d’heuristiques spécialisées, elles montrent généralement de moins bonnes performances.
Les métaheuristiques sont souvent employées en optimisation combinatoire, mais on en rencontre également pour des problèmes continus ou mixtes (problèmes à variables discrètes et continues).
Certaines métaheuristiques sont théoriquement « convergentes » sous certaines conditions. Il est alors garanti que l’optimum global sera trouvé en un temps fini, la probabilité de ce faire augmentant asymptotiquement avec le temps. Cette garantie revient à considérer que l’algorithme se comporte au pire comme une recherche aléatoire pure (la probabilité de tenter toutes les solutions tendant vers 1). Cependant, les conditions nécessaires sont rarement vérifiées dans le cadre d’applications réelles. En pratique, la principale condition de convergence est de considérer que l’algorithme est ergodique (qu’il peut atteindre n’importe quelle solution à chaque mouvement), mais on se satisfait souvent d’une quasi-ergodicité (si la métaheuristique peut atteindre n’importe quelle solution en un nombre fini de mouvements).
Organisation générale
D’une manière générale, les métaheuristiques s’articulent autour de plusieurs notions :
- Voisinage ;
- Diversification/exploration ;
- Intensification/exploitation ;
- Mémoire et apprentissage.
Voisinage
Le voisinage d'une solution est un sous-ensemble de solutions qu'il est possible d'atteindre par une série de transformations données. Par extension on désigne parfois par le terme « voisinage » l'ensemble des transformations considérées.
Un voisinage simple pour le problème du voyageur de commerce sera, par exemple, l'ensemble des solutions qu'il est possible de construire en permutant deux villes dans une solution donnée.
La notion de voisinage est sans doute le principe général le plus utilisé pour la conceptions d’heuristiques. Pour les problèmes combinatoires, le voisinage a un impact important sur le comportement des métaheuristiques, alors que pour des problèmes continus, la notion même de voisinage est plus difficile à cerner.
Bien qu’il n’existe que très peu de résultats théoriques sur l’adéquation entre un voisinage et un problème discret donné, il peut être possible d’en calculer des indicateurs empiriques, comme la rugosité. Les techniques les plus classiques concernant la définition d’un voisinage tournent autour des notions de permutations, de chaînes d’éjections et d’optimisations partielles.
Intensification, diversification, apprentissage
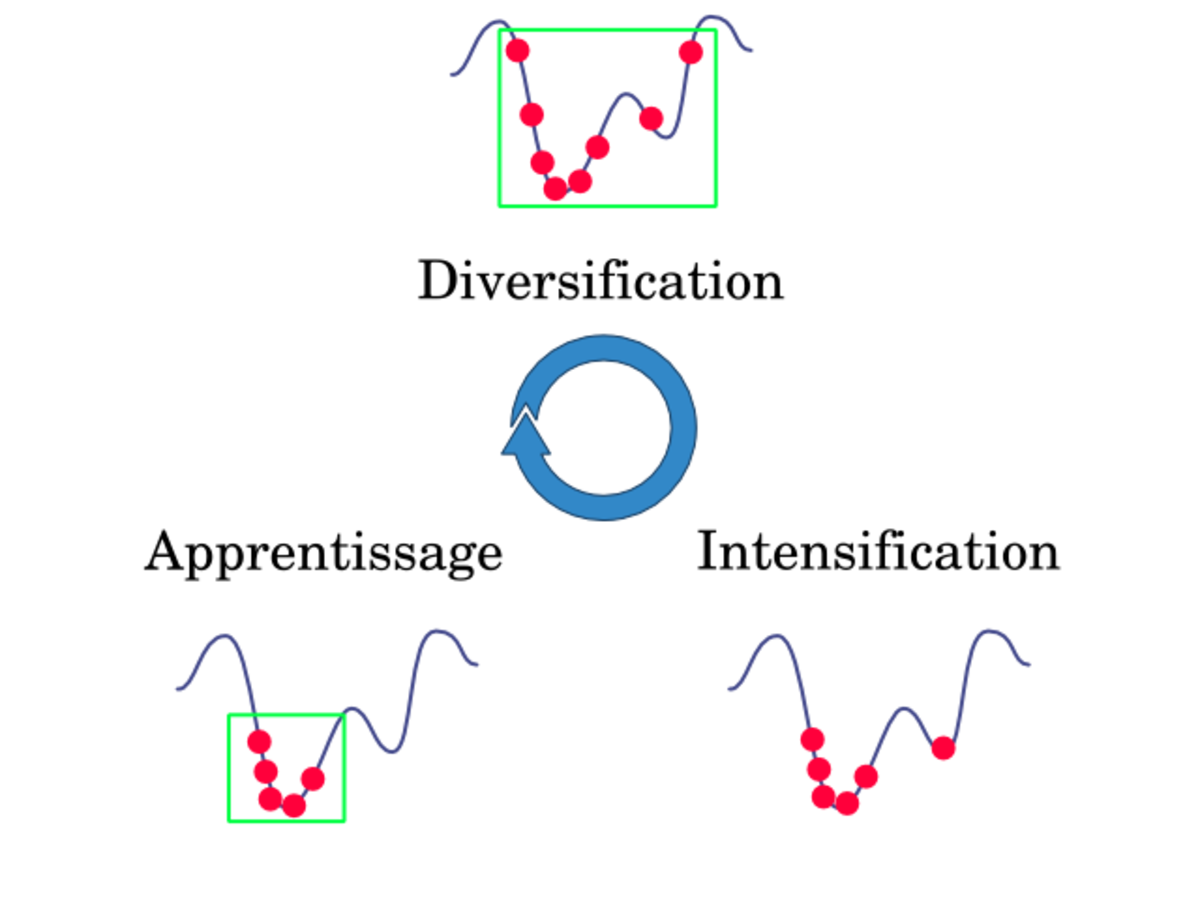
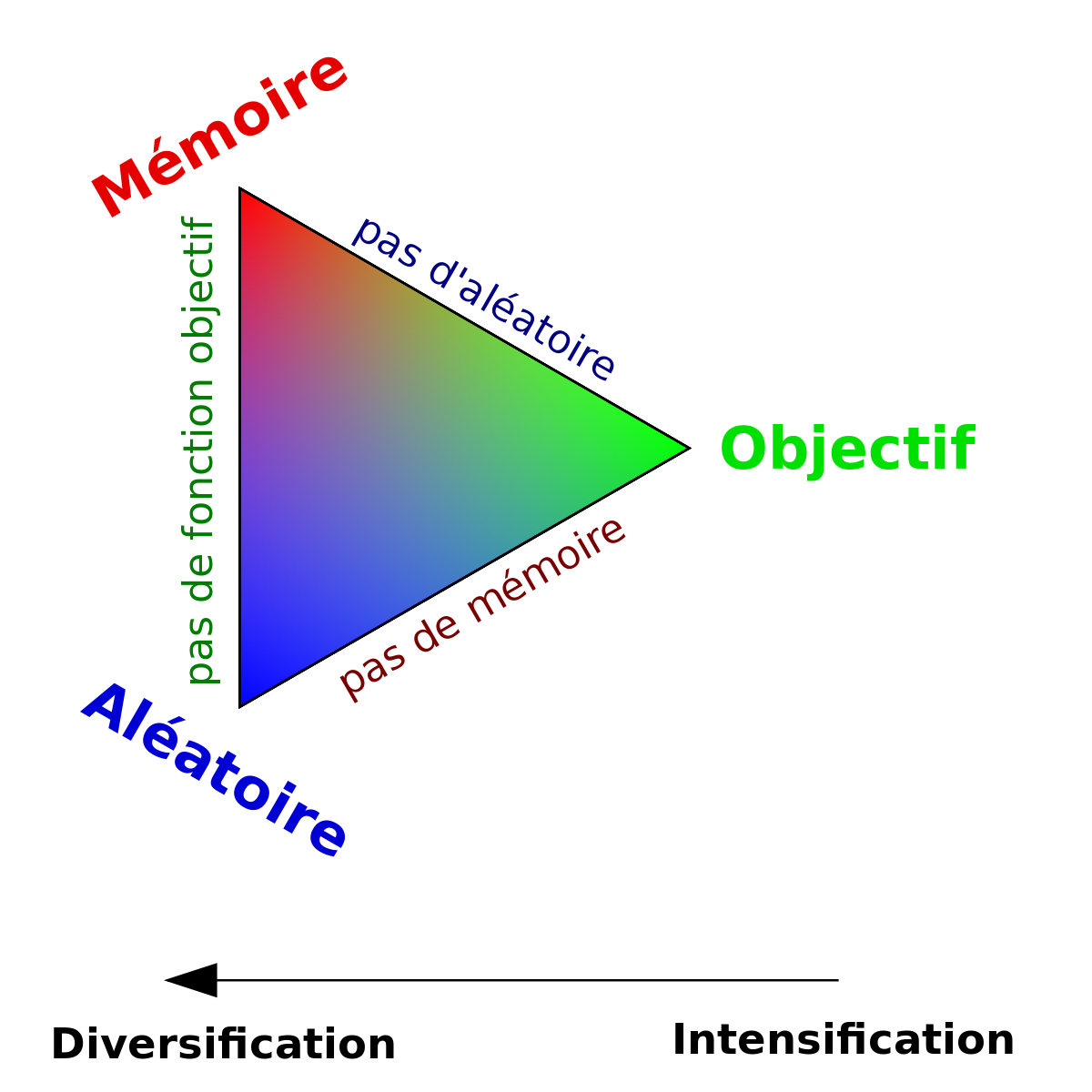
La diversification (ou exploration, synonyme utilisé presque indifféremment dans la littérature des algorithmes évolutionnaires) désigne les processus visant à récolter de l’information sur le problème optimisé. L'intensification (ou exploitation) vise à utiliser l’information déjà récoltée pour définir et parcourir les zones intéressantes de l’espace de recherche. La mémoire est le support de l’apprentissage, qui permet à l’algorithme de ne tenir compte que des zones où l’optimum global est susceptible de se trouver, évitant ainsi les optima locaux.
Les métaheuristiques progressent de façon itérative, en alternant des phases d’intensification, de diversification et d’apprentissage, ou en mélant ces notions de façon plus étroites. L’état de départ est souvent choisi aléatoirement, l’algorithme se déroulant ensuite jusqu’à ce qu’un critère d’arrêt soit atteint.
Les notions d’intensification et de diversifications sont prépondérantes dans la conception des métaheuristiques, qui doivent atteindre un équilibre délicat entre ces deux dynamiques de recherches. Les deux notions ne sont donc pas contradictoires, mais complémentaires, et il existe de nombreuses stratégies mélant à la fois l’un et l’autre des aspects.