Méthode de l'entropie croisée - Définition

Algorithme CE générique

1. Choisir un vecteur des paramètres initial ; poser t = 1.
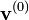
2. Générer un échantillon de variables aléatoires selon la densité
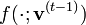
3. Calculer , où
   
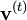
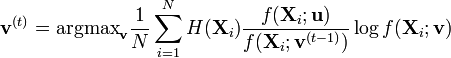
4. Si l'algorithme a convergé alors stopper; sinon, incrémenter t de 1 recommencer à l'étape 2.

Dans certains cas, la solution de l'étape 3 peut être trouvée analytiquement. Les situations où celà se produit sont

• Quand fait partie des fonctions de la  natural exponential family  ⇔  famille exponentielle
• Quand est discrète avec un support fini
• Quand et , alors correspond à l'estimateur du maximum de vraisemblance basé sur les .

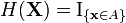
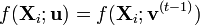
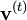
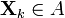
Méthodes liées

• Recuit simulé
• Algorithme génétique
• Algorithme à estimation de distribution
• Recherche tabou