Méthode de l'entropie croisée - Définition

Introduction

La méthode de l'entropie-croisée (CE) attribuée à Reuven Rubinstein est une méthode générale d'optimisation de type Monte-Carlo, combinatoire ou continue. La méthode a été conçue à l'origine pour la simulation d'événements rares, où des densités de probabilités très faibles doivent être estimées correctement, par exemple dans l'analyse de la sécurité des réseaux, les modèles de file d'attente, ou l'analyse des performances des systèmes de télécommunication. La méthode CE peut être appliquée à tout problème d'optimisation combinatoire où les observations sont bruitées comme le problème du voyageur de commerce, le problème d'affectation quadratique, le problème d'alignement de séquences, le problème de la coupure maximale et les problèmes d'allocation de mémoire, tout comme des problèmes d'optimisation continue avec de nombreux extrema locaux.

La méthode CE se décompose en deux phases :

1. Générer aléatoirement un échantillon de données (trajectoires, vecteurs, etc.) selon un mécanisme spécifique.
2. Mettre à jour les paramètres du mécanisme de génération aléatoire à partir de l'échantillon de données pour produire un meilleur échantillon à l'itération suivante. Cette étape implique de minimiser l'entropie croisée ou la divergence de Kullback-Leibler.

Estimation via l'échantillonnage préférentiel

Considérons le problème général d'estimation de la quantité , où H est une fonction objectif et est une densité de probabilité paramétrique. En utilisant l'échantillonnage préférentiel cette quantité peut être estimée par , où est un échantillon de variables aléatoires de densité . Pour H positif, l'optimum théorique de la densité de probabilité des variables aléatoires est donné par . Cependant est un paramètre inconnu. La méthode CE propose d'approcher la densité optimale en sélectionnant les éléments de l'échantillon qui sont les plus proches (au sens de Kullback-Leibler) de la densité optimale g ^* .

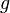
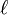
Optimisation continue—exemple

Le même algorithme CE peut être utilisé pour l'optimisation et l'estimation. Soit le problème consistant à maximiser une fonction S(x), par exemple, . Pour utiliser l'entropie croisée on doit d'abord considérer le problème stochastique associé de l'estimation de pour un niveau donné , et une famille de distributions de probabilité paramètriques , par exemple la loi normale à une dimension, dont les parmètres sont la moyenne et la variance (tel que ici). Ainsi, pour un donné, l'objectif est de déterminer tel que la quantité soit minimisée. Ce qui est fait en utilisant la version échantillonnée ( stochastic counterpart  ⇔  contrepartie stochastique) du problème de la minimisation de la divergence KL, comme précédemment dans l'étape 3. Il se trouve que pour ce choix de distribution les paramètres qui minimisent la version stochastique du problème sont la moyenne et la variance empirique de l'échantillon d'élite qui est composé des tirages dont la valeur de la fonction score est . Le plus mauvais des éléments de l'échantillon d'élite sert de paramètre de niveau à l'itération suivante. Cela donne l'algorithme stochastique suivant pour ce problème.

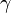
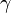
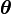
Pseudo-code

      1. mu:=-6; sigma2:=100; t:=0; maxits=100;    // Initialisation des paramètres      2. N:=100; Ne:=10;                           //      3. while t < maxits and sigma2 > epsilon     // Tant que l'on a pas convergé et que maxits n'est pas dépassé      4.  X = SampleGaussian(mu, sigma2,N);         // Génère N échantillon à partir de la distribution      5.  S = exp(-(X-2)^2) + 0.8 exp(-(X+2)^2);   // Calcule le score de chaque échantillon      6.  X = sort(X, S);                           // Classe X selon le score (de façon descendante)      7.  mu = mean(X(1:Ne)); sigma2=var(X(1:Ne)); // Mise à jour des parmètres de la distribution      8.  t = t+1;                                 // Incrémentation du nombre d'itérations      9. return mu                                 // Renvoie la moyenne des derniers échantillons comme la solution