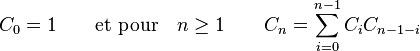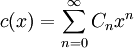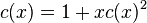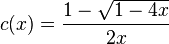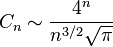Nombres de Catalan - Définition

Histoire

La suite de Catalan fut décrite pour la première fois au XVIII^e siècle par Leonhard Euler, qui s'était intéressé au nombre de différentes façons de partager un polygone en triangles. La première publication sur ces nombres est due à Segner et la suite porte alors le nom de Nombre de Segner. Eugène Charles Catalan fit le lien avec le nombre d'expressions « parenthésées » et le nom de Catalan remplaça celui de Segner. L'astuce de comptage des mots de Dyck fut trouvée par Désiré André en 1887.

Relation de récurrence et comportement asymptotique

Les nombres de Catalan satisfont la relation de récurrence

Ceci vient du fait que tout mot de Dyck w de longueur supérieure à 2 peut s'écrire de manière unique sous la forme

w = Xw₁Yw₂,

où w₁ et w₂ désignent des mots de Dyck (éventuellement vides). La fonction génératrice des nombres de Catalan est définie par

et en utilisant la relation de récurrence ci-dessus nous voyons que

et par conséquent

Asymptotiquement, les nombres de Catalan se comportent comme