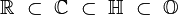Octonion - Définition

Sous-algèbres particulières

On vérifie aisément que toutes les opérations dans la sous-algèbre des octonions dont la partie imaginaire est nulle sont équivalentes aux opérations dans l’algèbre des réels. De même la sous-algèbre des octonions dont toutes les dimensions réelles sauf les 2 premières sont nulles est équivalente à l’algèbre des complexes. De même la sous-algèbre des octonions dont toutes les dimensions réelles sauf les 4 premières sont nulles est équivalente à l’algèbre des quaternions.

Par conséquent on identifiera les nombres réels, complexes et quaternions comme des octonions particuliers, qu’on notera de la même façon : .