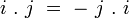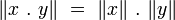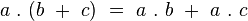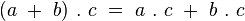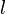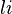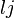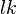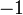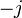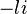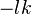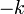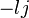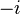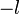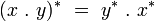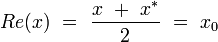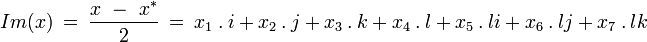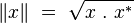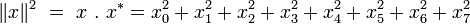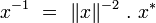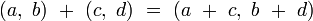Octonion - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, les octonions ou octaves sont une extension non-associative des quaternions. Ils forment une algèbre à 8 dimensions sur les réels. L’algèbre des octonions est généralement notée
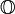
En perdant l’importante propriété d’associativité, les octonions ont reçu moins d’attention que les quaternions. Malgré cela, les octonions gardent leur importance en algèbre et en géométrie, notamment parmi les groupes de Lie.
Historique
Les octonions ont été découverts en 1843 par John T. Graves, un ami de William Hamilton, qui les appela octaves. Ils furent découverts indépendamment par Arthur Cayley, qui publia le premier article sur le sujet en 1845. Ils sont souvent appelés octaves de Cayley ou algèbre de Cayley.
Propriétés
La multiplication des octonions n'est ni commutative :
ni associative :
-
Elle satisfait une forme plus faible que l’associativité : l’alternativité. Cela signifie que la sous-algèbre générée par 2 éléments quelconques
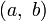
-
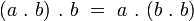
On peut montrer que la sous-algèbre générée par 2 éléments quelconques de
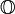


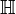
Les octonions partagent une propriété importante avec


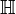
Cela implique que les octonions forment une algèbre de division normée non-associative. Les algèbres de plus haute dimensions définies par la construction de Cayley-Dickson (par exemple les sédénions) ne satisfont pas cette propriété : elles ont toutes des diviseurs de zéro et leurs multiplications ne satisfont plus la conservation des normes.
Il s’avère que les seules algèbres de division normées sur les réels sont


La multiplication des octonions n’étant pas associative, les éléments de
Automorphismes
Un automorphisme
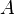
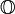
-
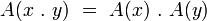
L’ensemble des automorphismes de
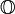
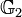
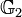
Définition
Chaque octonion est une combinaison linéaire à coefficients réels d’octonions unitaires
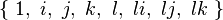
Autrement dit, chaque octonion
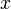
-
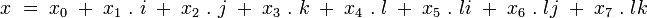
avec des coefficients réels
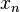
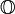
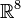
Addition
L’addition des octonions se réalise en additionnant les coefficients correspondants, comme pour les nombres complexes et les quaternions :
-
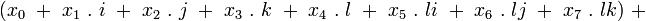
-
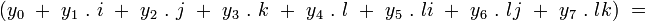
-
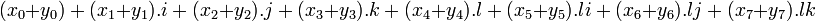
Propriétés
L’addition des octonions est commutative :
-
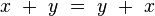
associative :
-
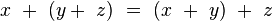
et a un élément neutre, zéro, noté
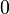
-
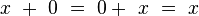
Pour tout octonion
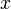
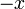
-
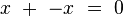
- Cet octonion, nommé opposé, s'obtient simplement en prenant l'opposé des coefficients réels de
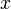
Ainsi l'ensemble des octonions muni de l'addition et de l'opposé est un groupe commutatif.
Soustraction
La soustraction des octonions est alors l'opération simplement définie par :
-
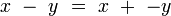
Multiplication
La multiplication des octonions est alors complètement déterminée par la propriété de distributivité à droite et à gauche :
où
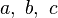
| . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dans la table ci-dessus, l’opérande de gauche est indiqué dans la première colonne, et l’opérande de droite est dans la première rangée. Le tableau n'est pas symétrique, ce qui signifie que cette multiplication n'est pas commutative.
La table de multiplication peut être définie entièrement par l'identité remarquable :
-
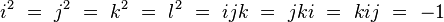
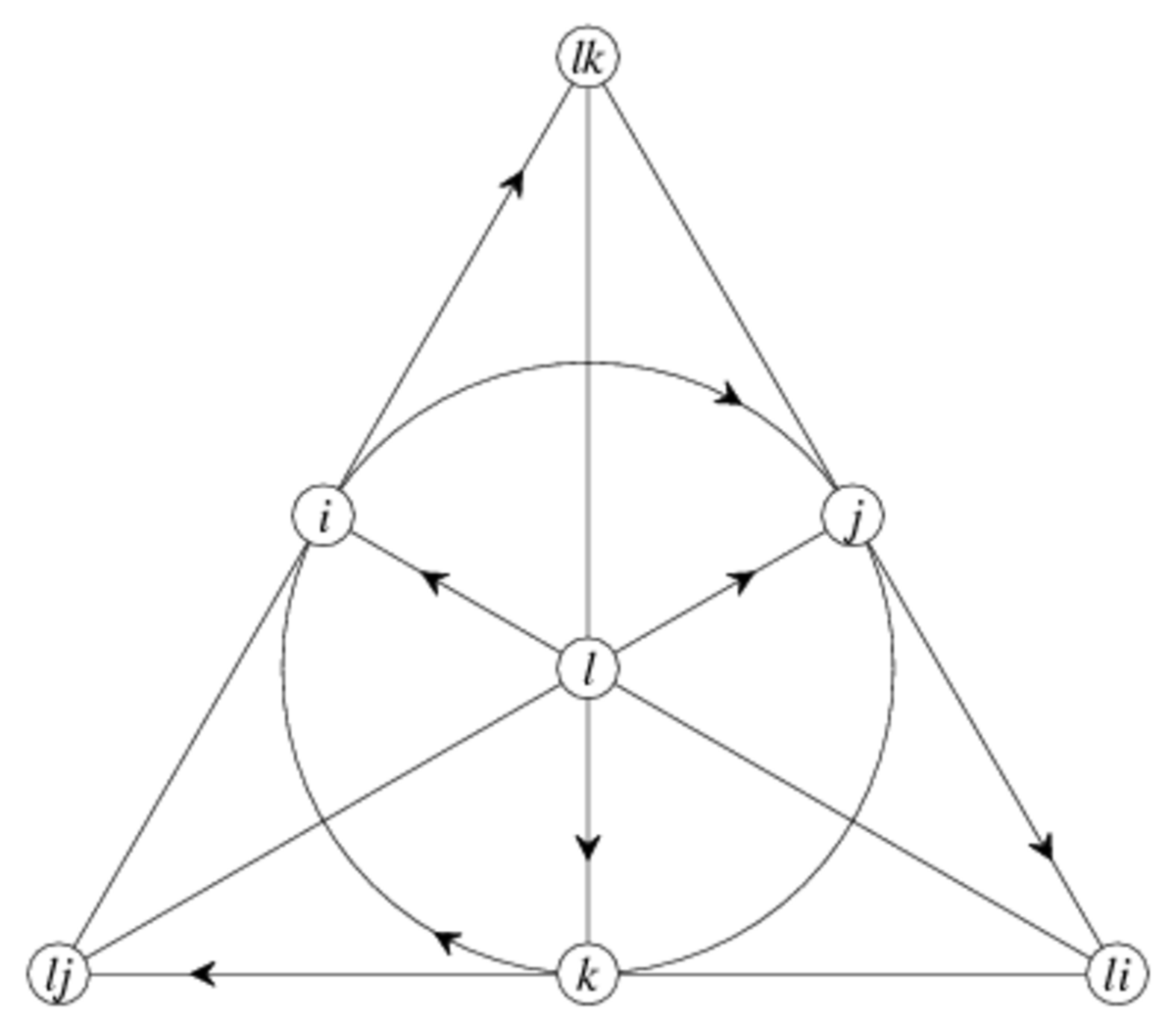
Plan mnémotechnique de Fano
Un moyen mnémotechnique pour se rappeler les produits des octonions unitaires est donné par le diagramme ci-contre.
Ce diagramme à 7 points et 7 droites (le cercle passant par
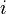
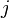
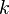
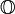
Soit
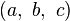
-
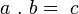
-
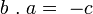
avec des permutations cycliques. Celles-ci opèrent de la manière suivante :
-
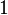
-
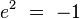

Chacune des 7 droites génère une sous-algèbre de
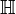
Conjugué
Le conjugué d'un octonion
-
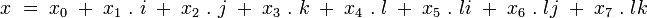
est donné par
-
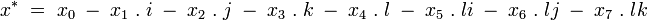
La conjugaison est une involution de
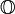
(notons le changement dans l’ordre de succession).
Parties réelle et imaginaire
La partie réelle de l’octonion
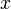
et la partie imaginaire
de sorte que pour tout octonion
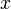
-
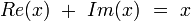
-
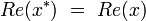
-
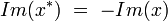
L’ensemble de tous les octonions purement imaginaires (dont la partie réelle est nulle) forme une sous-espace à 7 dimensions sur les réels de
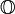
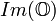
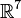
L’ensemble de tous les octonions purement réels (dont la partie imaginaire est nulle) forme une sous-algèbre à 1 dimension de
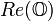

Norme
La norme d’un octonion
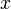
Cette racine carrée est bien un nombre réel positif :
Cette norme correspond à la norme euclidienne sur
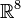
On a aussi:
-
![\|x\|\ =\ \sqrt{[Re(x)]^2\ -\ [Im(x)]^2}](https://static.techno-science.net/illustration/Definitions/autres/5/5cf288ef37df439ca6f02b634c0d6713_6fd3bf095ddbe110f4bcbd6fdf13ac0f.png)
-
![Re(x)\ =\ \pm\sqrt{[Im(x)]^2 + \|x\|^2}](https://static.techno-science.net/illustration/Definitions/autres/5/5b5f63f06ed3848e1f781cc09136c1c9_3cb53ef24fdf8420e7955632b169256a.png)
-
![[Im(x)]^2\ =\ [Re(x)]^2 - \|x\|^2](https://static.techno-science.net/illustration/Definitions/autres/b/bba3af35af9c2a4ad7d302702c43e15a_40e6ec1ace847d09f51078fa5ae47343.png)
Inverse
L’existence d’une norme sur
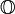
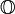
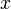
Cela satisfait
-
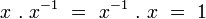
L'ensemble
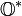
Division
La division des octonions
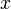
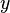
-
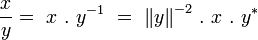
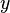
Construction de Cayley-Dickson
A l’instar des quaternions assimilés aux couples de nombres complexes (et des nombres complexes assimilés aux couples de nombres réels), les octonions peuvent être traités sous forme de couples de quaternions.
L’addition de couples de quaternions
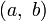
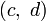
La multiplication de 2 couples de quaternions
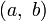
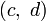
où
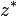
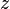
La multiplication d'un nombre réel
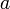
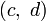
-
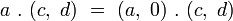
-
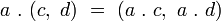
On peut alors définir l’algèbre des couples de quaternions par l'ensemble
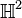
-
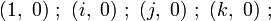
-
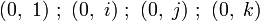
Cet ensemble, muni des opérations ci-dessus forme une algèbre à 2 dimensions sur l'ensemble des quaternions, et à 8 dimensions sur l'ensemble des nombres réels.
Soit
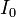
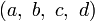
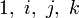
On montre facilement que l’opération I suivante, qui associe tout couple de quaternions
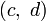
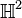
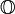
-
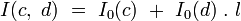
Il s'ensuit que
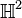
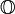
On démontre alors que les additions et multiplications d’octonions
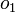
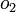
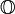
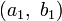
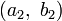
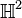
-
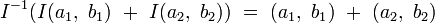
-
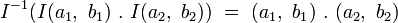
-
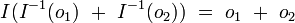
-
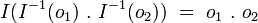
Par suite, on pourra simplement définir les octonions au moyen de couples de quaternions, en incluant les quaternions dans l'ensemble des octonions munis des opérations de la construction de Cayley-Dickinson et des égalités suivantes :
-
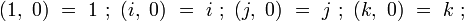
-
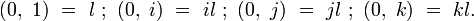
(dans ce cas, l’isomorphisme I ci-dessus qui devient une simple identité.)