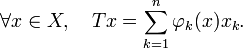Opérateur compact - Définition

Exemples

Opérateurs de rang fini

Soit X un espace de Banach, et T un opérateur borné sur X. On dit que T est un opérateur de rang fini si ImT est un espace de dimension finie. Il existe alors un entier naturel , des formes linéaires continues et des vecteurs tels que

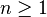
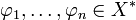
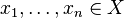
Les opérateurs de rang fini sont compacts car dans un espace de dimension finie, les parties compactes sont les parties fermées bornées. Ainsi, si X est de dimension finie, tout opérateur borné sur X est compact, car de rang fini. Remarquons que l’ensemble des opérateurs compacts étant fermé, tout opérateur qui est limite dans B(X) d’opérateurs de rang fini est compact . Cependant, un opérateur compact n’est pas nécessairement limite d’opérateurs de rang fini. Si X vérifie la propriété "tout opérateur compact est limite d'opérateurs de rang fini", on dit que X a la propriété d’approximation. Citons par exemple les espaces ayant une base de Schauder, comme les espaces L_p([0,1]), 1 ≤ p < +∞, ou les espaces de Hilbert séparables.

Opérateurs à noyau

Opérateurs compacts dans les espaces de Hilbert