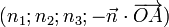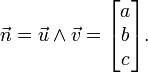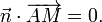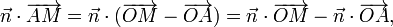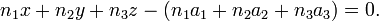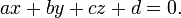Plan (mathématiques) - Définition
La liste des auteurs de cet article est disponible ici.
Équations dans un espace de dimension 3
Définition par deux vecteurs et un point
Soit un point A(a1;a2;a3) par lequel passe le plan
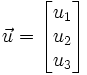
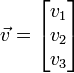
Equations paramétriques
Le plan
-
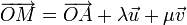
ou
-
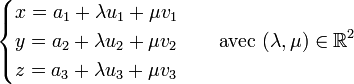
Equation cartésienne
Soit M(x;y;z) un point quelconque du plan et
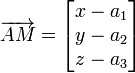
Pour que ces trois vecteurs soient coplanaires, il faut que leur produit mixte soit nul :
-
![0=[\vec u,\vec v,\overrightarrow{AM}]=[\vec u,\vec v,\overrightarrow{OM}]-[\vec u,\vec v,\overrightarrow{OA}]](https://static.techno-science.net/illustration/Definitions/autres/d/dddcf6dee5bf8320b370bb60b2d5d853_fc980097eccaef0f15608ba0900b5b64.png)
-
![[\vec u,\vec v,\overrightarrow{OM}]=\begin{vmatrix} u_1 && v_1 &&x\\ u_2 && v_2 && y\\ u_3 && v_3&& z \end{vmatrix}=\underbrace{(u_2v_3 - u_3v_2)}_ax +\underbrace{(u_3v_1 - u_1v_3)}_by +\underbrace{(u_1v_2 - u_2v_1)}_cz](https://static.techno-science.net/illustration/Definitions/autres/9/9f5ad7c6f9fccdc2efaafad65267685c_a7dc6ce50c90fa64245a05269f6f6f07.png)
-
![-[\vec u,\vec v,\overrightarrow{OA}]=\underbrace{-(aa_1+ba_2+ca_3)}_d.](https://static.techno-science.net/illustration/Definitions/autres/7/7e0e3dac2d904c86a4d60d4413ff9733_2ff158ace85563a721fa4b565c99c3d0.png)
![0=[\vec u,\vec v,\overrightarrow{AM}]=[\vec u,\vec v,\overrightarrow{OM}]-[\vec u,\vec v,\overrightarrow{OA}]](https://static.techno-science.net/illustrationWebp/Definitions/autres/d/dddcf6dee5bf8320b370bb60b2d5d853_fc980097eccaef0f15608ba0900b5b64.png)
![[\vec u,\vec v,\overrightarrow{OM}]=\begin{vmatrix} u_1 && v_1 &&x\\ u_2 && v_2 && y\\ u_3 && v_3&& z \end{vmatrix}=\underbrace{(u_2v_3 - u_3v_2)}_ax +\underbrace{(u_3v_1 - u_1v_3)}_by +\underbrace{(u_1v_2 - u_2v_1)}_cz](https://static.techno-science.net/illustrationWebp/Definitions/autres/9/9f5ad7c6f9fccdc2efaafad65267685c_a7dc6ce50c90fa64245a05269f6f6f07.png)
![-[\vec u,\vec v,\overrightarrow{OA}]=\underbrace{-(aa_1+ba_2+ca_3)}_d.](https://static.techno-science.net/illustrationWebp/Definitions/autres/7/7e0e3dac2d904c86a4d60d4413ff9733_2ff158ace85563a721fa4b565c99c3d0.png)
On distingue 4 facteurs que nous appellerons
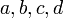
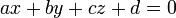
Dans le cadre euclidien, nous remarquons en outre que les nombres a,b et c sont les composantes du vecteur
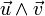
![\left[\vec u, \vec v, \vec w\right] = (\vec u \wedge \vec v) \cdot \vec w\,](https://static.techno-science.net/illustrationWebp/Definitions/autres/e/e3e94bd42adeb89556d444a062b694c4_235383d7f0e8425cce4294ee0e759328.png)
Définition par un vecteur normal et un point
Le plan passant par
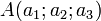
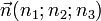
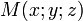
En utilisant les égalités
cette définition équivaut à l'équation cartésienne :
On identifie généralement le quadruplet
