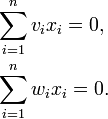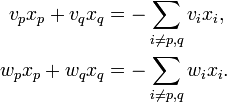Plan (mathématiques) - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, un plan est un objet fondamental à deux dimensions. Intuitivement il peut être visualisé comme une feuille d'épaisseur nulle qui s'étend à l'infini. L'essentiel du travail fondamental en géométrie et en trigonométrie s'effectue en deux dimensions donc dans un plan.
Définitions
Dans les Éléments d'Euclide, seule la notion de figure plane est définie. Une figure plane est une figure contenue dans la surface balayée par une droite dont un point est fixé et le second assujetti à se déplacer sur une seconde droite. Cette définition repose malheureusement sur la définition donnée de surface qui manquait de précision. Dans la présentation actuelle des mathématiques, un plan vectoriel ou affine est défini comme un objet de l'algèbre linéaire :
Un Plan (vectoriel ou affine) est un K-espace vectoriel ou un K-espace affine de dimension deux, où K désigne un corps.
Le cas le plus fréquent correspond à celui où le corps K est celui des nombres réels. Ainsi le plan complexe désigne le corps des nombres complexes considéré comme un espace vectoriel de dimension deux sur le corps des réels.
Un cas important est celui où un plan désigne un sous-espace affine de dimension deux dans un espace de dimension trois sur le corps des réels. Cette situation modélise simplement notre géométrie.
Il existe alors de nombreuses manières de définir un plan, notamment :
- le plus petit espace affine contenant trois points non alignés ;
- le plus petit espace affine contenant une droite et un point n'appartenant pas à cette droite ;
- le plus petit espace affine contenant deux droites non confondues et sécantes ;
- le plus petit espace affine contenant deux droites non confondues et parallèles ;
- le plus petit espace affine contenant un point et dont la direction est engendrée par deux deux vecteurs non colinéaires ;
- le plus petit espace affine contenant un point et orthogonal à un vecteur non nul, le vecteur normal.
Par la suite, nous utiliserons les deux dernières définitions pour l'élaboration des équations du plan.
Positions relatives d'un plan et d'une droite
Étant donnés (D) une droite et un plan (P), les différentes positions relatives sont :
- (D) est incluse dans(P) ;
- l'intersection de(D) et de (P) est réduite à un point ;
- (D) et (P) sont disjoints.
Dans un espace de dimension trois, (D) est parallèle à (P) si et seulement si (D) est incluse dans (P) ou disjointe de (P).
Positions relatives de deux plans
Dans un espace de dimension trois, il n'existe que deux positions relatives de deux plans :
- parallèles : strictement (intersection vide) ou bien confondus;
- sécants : leur intersection est alors une droite. Ils peuvent être orthogonaux (leurs vecteurs « normaux » sont orthogonaux)
Géométrie vectorielle
Un plan est un sous-espace de dimension 2 d'un espace vectoriel sur un corps
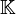
Un plan est toujours engendré par deux vecteurs v et w non colinéaires. De la sorte, x est un vecteur du plan si et seulement s'il est combinaison linéaire de v et w, à coefficients dans
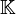
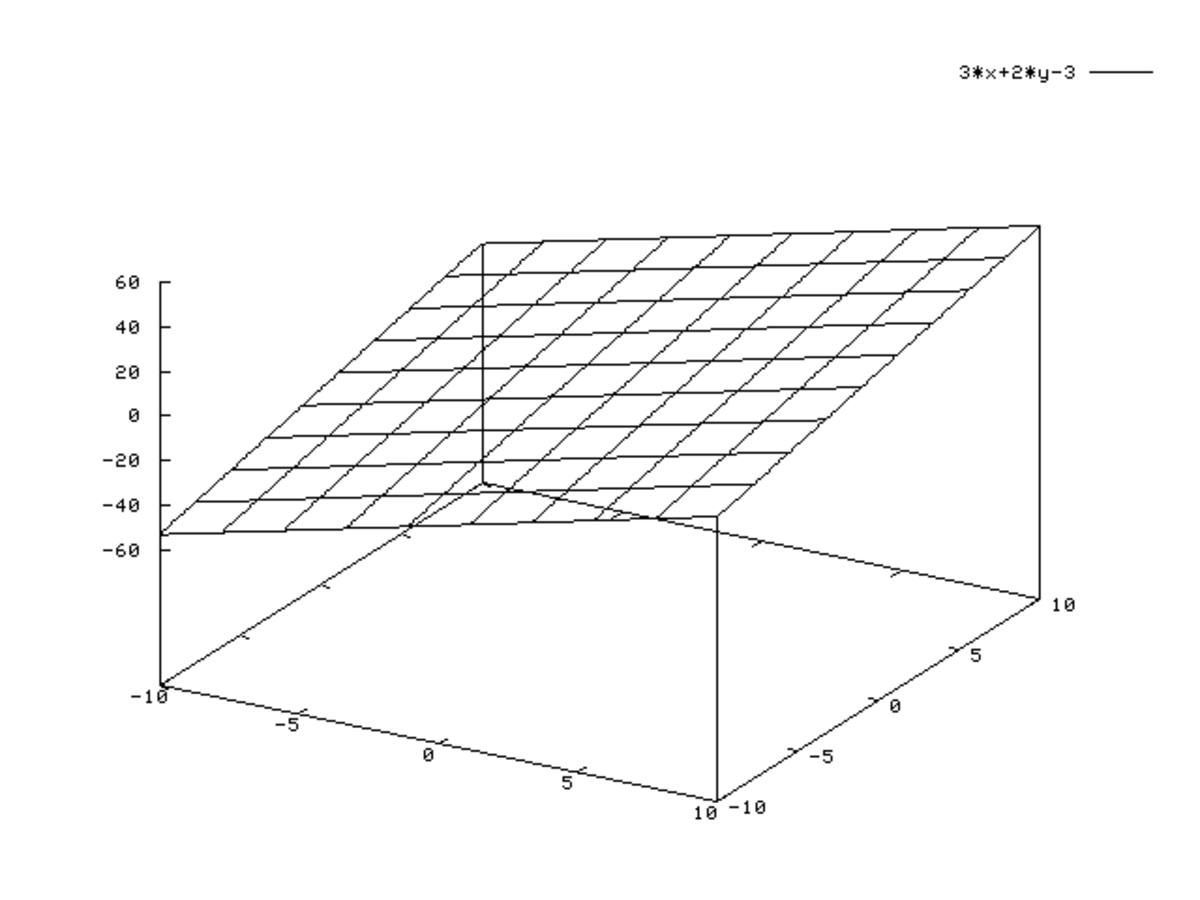
Approche analytique en dimension 3
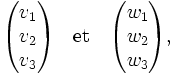
Dans le cas où l'espace V est de dimension 3, il suffit d'une seule forme linéaire pour définir un plan. Connaissant deux vecteurs v et w qui l'engendrent, de coordonnées
il est utile de savoir fabriquer une forme linéaire donnant l'équation du plan. Le produit mixte de v, w et z est nul si et seulement si z appartient au plan engendré par v et w. Ce produit mixte s'écrit
On a ainsi obtenu la forme linéaire désirée.
Réciproquement, si on possède une forme linéaire
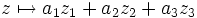
- z2 = − (a1z1 + a3z3) / a2.
Alors en substituant au couple (z1,z3) les couples indépendants (1,0) et (0,1), on obtient deux vecteurs
qui sont forcément indépendants puisque leurs projections respectives sur le plan des z1,z3 par rapport à l'axe des z2 sont des vecteurs indépendants.
Généralisation en dimension plus élevée
Supposons qu'on ait dans un espace de dimension n deux vecteurs v et w indépendants. Comment trouver n − 2 formes linéaires indépendantes donnant les équations du plan? Cela revient à chercher une base de solutions du système linéaire
Pour ce faire, on sélectionne deux indices p et q tels que les couples (vp,vq) et (wp,wq) soient linéairement indépendants. Géométriquement, cela revient à sélectionner un plan de coordonnées tel que la projections respaectives de v et w sur ce plan, parallèlement au sous-espaces{z:zp = zq = 0} soient indépendantes. Un tel plan existe toujours parce que v et w sont indépendants. Une fois ceci fait, on réécrit le système précédent sous la forme
La solution de ce système linéaire est obtenue par les méthodes classiques. Pour obtenir une base de l'espace des solutions, il suffira de substituer à la suite à n − 2 éléments
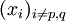
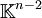
-
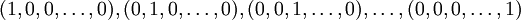
Réciproquement, étant données n − 2 formes linéaires indépendantes
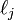
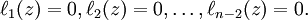
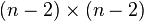
\cdot z=z_1(v_2w_3-v_3w_2)+z_2(v_3w_1-v_1w_3)+z_3(v_1w_2-v_2w_3).](https://static.techno-science.net/illustration/Definitions/autres/d/df4876d3081c25c108c8dc936a1e622b_3e0f38ba0eac58cca9a363615abf7dc9.png)