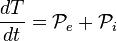Principe des puissances virtuelles - Définition
La liste des auteurs de cet article est disponible ici.
Principe des puissances virtuelles et théorèmes fondamentaux de la mécanique
Le Principe des puissances virtuelles (PPV) permet de retrouver entre autres le principe fondamental de la dynamique et le théorème de l'énergie cinétique.
Principe fondamental de la dynamique
Si l'on applique le PPV à un solide soumis aux efforts volumiques f et surfaciques F en choisissant un champ rigidifiant
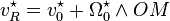
![\int_\Omega [(f\cdot v_0^\star) + (OM\wedge f)\cdot\Omega_0^\star ]d\Omega \;+ \int_{\partial\Omega} [F\cdot v_0^\star + \Omega_0^\star\cdot(OM\wedge F)]dS = \int_\Omega \rho\left[\gamma\cdot(v_0^\star + OM\wedge \Omega_0^\star)\right]d\Omega](https://static.techno-science.net/illustration/Definitions/autres/9/9f93c0e9d74b944e6875ad5b0e05b7fe_d9884ed13eb5e4ecf35cba91d6503584.png)
Ce qui traduit le fait que la réduction du torseur des actions extérieures en O – point fixe – est égale à la dérivée de la réduction du torseur cinétique au même point :
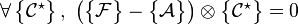
Où
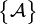
et
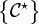
Théorème de l'énergie cinétique
Pour retrouver le théorème de l'énergie cinétique (notée T ici), il suffit de choisir comme mouvement virtuel le mouvement réel, on obtient alors immédiatement :