Principe des puissances virtuelles - Définition

Introduction

Le principe des puissances virtuelles ou PPV est un principe fondamental en mécanique, qui postule un équilibre de puissance dans un mouvement virtuel, il s'agit d'une formulation duale du PFD. Il permet de retrouver certains principes ou théorèmes comme le principe fondamental de la dynamique et le théorème de l'énergie cinétique, et constitue aussi la base d'une démarche de modélisation pour les milieux continus (théorie du premier gradient, théorie du second gradient). On parle parfois du principe des travaux virtuels ou PTV qui est sensiblement le même principe.

Approche vulgarisée

Le principe de base est le suivant : si un solide est à l'équilibre (statique du solide), la somme des efforts est nulle. Donc si l'on fait faire un déplacement fictif (virtuel) à l'objet, la somme des puissances des forces et moments est nulle.

Ce principe permet parfois des calculs plus simples, en particulier en théorie des plaques.

En pratique, l'estimation des efforts appliqués à un système se fait toujours par l'intermédiaire d'un déplacement (ou déformation) de ce système :

• On soulève légèrement une valise pour connaître son poids.
• On presse sur le pneu du vélo, pour savoir si la pression de la chambre à air est suffisante.
• L'oculiste déforme légèrement la cornée de l'œil pour mesurer la pression intraoculaire.
• Avant de mettre en service un pont, on le charge par plusieurs camions et on mesure les petites déformations qui doivent être compatibles avec celles calculées par les codes de calcul.

Si idéalement, on effectue les expériences précédentes en des temps de plus en plus brefs, on passe à la limite; on obtient la mesure des efforts par la mesure des puissances mises en œuvre, pour les vitesses ayant servi de tests (vitesses virtuelles).

Exemple de la statique et de la dynamique d'un point matériel unique

Soit M un point matériel de masse m en équilibre par rapport à un repère galiléen . On note F la résultante des forces extérieures. Si est un vecteur quelconque de l'espace , l'équation classique de la statique du point :

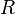
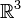
F = 0

est équivalente à :

Le produit est appelé la puissance virtuelle de la force F par rapport à .

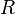
Si le point M est en mouvement par rapport à , on note l'accélération du point par rapport à ce repère.

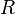
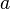
L'équation classique de la dynamique de M

F = ma

est équivalente à

Le produit est appelé puissance virtuelle des quantités d'accélération par rapport à .

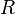
Énoncé

N'est présenté ici que l'aspect le plus classique du PPV, à savoir celui où le champ cinématique est virtuel. On peut tout aussi bien développer ce principe avec un champ d'effort virtuel, mais la notion de champ d'effort admissible est plus lourde à mettre en place et moins intuitive.

Notations et définitions

Système mécanique

Un système mécanique Ω est défini par un domaine de l'espace que l'on décide d'étudier.

Exemples de systèmes mécaniques :

1. un point matériel
2. un solide indéformable
3. un système de solides indéformables
4. un milieu continu (solide déformable ou fluide).

Mouvement admissible d'un système mécanique

Soit Ω un système mécanique, on appelle mouvement admissible de Ω la donnée d'un champ de vitesse en tout point du domaine du système, compatible avec les mouvements possibles du système.

• Pour un point matériel dans l'espace sans conditions particulières, les mouvements admissibles sont les translations de l'espace.
• Pour un solide indéformable, il s'agit des translations et des rotations.
• Pour un milieu continu, on a, a priori n'importe quel champ de vitesse continu (voire discontinu si l'on veut pouvoir étudier la rupture).

Mouvement rigidifiant d'un système mécanique

Un mouvement rigidifiant d'un système Ω est un mouvement conférant au système un mouvement de corps rigide.

Si l'on considère un système dans l'espace et que O est l'origine d'un repère spatial, alors tout mouvement rigidifiant peut s'écrire :

où et sont des vecteurs uniformes

Puissance accélératrice

La puissance accélératrice d'un système Ω est la puissance développée par les quantités d'accélération dans le champ de mouvement.

Pour un point matériel de masse m dans le champ de vitesse on obtient :

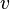
Pour un système de N points matériels de masses m_i on obtient dans le champ v_i :

Dans le cas d'un milieux continu (solides, fluides, etc.) de masse volumique ρ(M) dans un champ v(M) :

Puissance des efforts extérieurs

La puissance extérieure ou puissance des efforts extérieurs est la puissance développée par les efforts extérieurs dans le champ de vitesse.

Pour un point matériel soumis à la force F dans le champ de vitesse v elle s'exprime par :

Pour un système de N points P_i soumis aux forces F_i dans le champ v_i :

Pour un milieu continu Ω de frontière soumis aux efforts volumiques f(M) et aux efforts surfaciques F(M) dans le champ v(M):

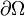
Puissance des efforts intérieurs

La puissance des efforts intérieurs est la puissance développée par les efforts intérieurs (ou internes) au système considéré. Ce sont le plus souvent des efforts de contact (systèmes de points matériels ou de solides, milieux granulaires) ou des efforts de cohésion (milieux continus).

Pour un point matériel ou un solide indéformable, cette puissance est toujours nulle. Pour un système de points matériels ou de solides, elle peut s'exprimer de manière similaire à la puissance extérieure (en considérant les actions sur chacun des points/solides par les autres).

Pour un milieu continu, son expression dépend de la modélisation adoptée et peut être déduite du PPV et de quelques hypothèses de modélisation.

Énoncé

Soit un référentiel galiléen. Les vitesses, accélérations et puissances sont prises par rapport à ce repère.

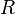
• Soit Ω un système, soit un espace, dit espace des mouvements virtuels, qui contient l'ensemble des mouvements admissibles par Ω et l'espace des mouvements virtuels rigidifiants. On note respectivement et la puissance accélératrice, la puissance des efforts extérieurs à Ω et la puissance des efforts intérieurs.

• Pour un système de points matériels quelconque, la puissance virtuelle d’accélération est égal à la somme des puissances virtuelles des efforts extérieurs et des efforts intérieurs, et la puissance virtuelle des efforts intérieurs dans un mouvement virtuel rigidifiant est nulle.