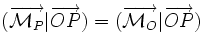Torseur - Définition

Introduction

Un torseur est un outil mathématique utilisé principalement en mécanique du solide indéformable, pour décrire les mouvements des solides et les actions mécaniques qu'ils subissent de la part d'un environnement extérieur.

Définition

Un torseur est un champ de vecteurs équiprojectif, champ dont les vecteurs en chaque point P s'appellent « moments » du torseur. De par les propriétés d'un tel champ, les moments en deux points P et O vérifient la relation de Varignon : . Un moyen mnémotechnique de la retenir est la dénomination "formule de BABAR" : , où le vecteur (associé de façon unique à tout champ équiprojectif), s'appelle résultante du torseur. Un torseur est donc déterminé par deux vecteurs, constituant sa "réduction" en un point quelconque P de l'espace, à savoir :

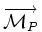
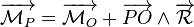
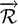
• La résultante . Ce vecteur est unique et indépendant du point de réduction.
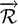
• Le moment en P du torseur, .

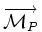
La résultante est un vecteur caractéristique du champ qui permet, à partir du moment en un point particulier, de retrouver les autres moments. De ce fait, les torseurs forment parmi les champs de vecteurs un sous-espace de dimension 6 (dans le cas de l'espace physique de dimension 3).

On écrit alors :

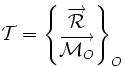
ou, en projetant la résultante et le moment sur une base orthonormée  :

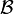
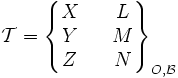
où X, Y, Z sont les coordonnées de la résultante et L, M, N les coordonnées du moment. Ces coordonnées sont appelées « coordonnées plückeriennes », du mathématicien allemand Julius Plücker.

Propriétés des torseurs

Équiprojectivité

Soit un torseur de résultante et de moment en O. Son moment en P est , de sorte que, en faisant le produit scalaire par , on obtient :

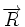
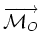
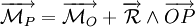
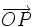
Cette relation s'appelle propriété d'équiprojectivité du champ. On montre que cette propriété est caractéristique des champs de torseurs. Autrement dit, si un champ de vecteurs est équiprojectif, alors il s'agit du champ des moments d'un torseur. C'est d'ailleurs la façon la plus fondamentale de définir un torseur.

L'équiprojectivité du champ des vitesses d'un solide indéformable est la propriété fondamentale décrivant le comportement cinématique de ces corps.

Cette relation est appelée aussi loi de transfert des moments puisqu'on obtient le moment du torseur au point P en utilisant celui en O tant que O et P appartiennent au même solide indéformable.

Axe d'un torseur

Considérons un torseur de résultante non nulle. Alors on montre que les points P tels que soit colinéaire à forment une droite appelée axe central d'un torseur. Cet axe central existe et est unique pour tout torseur, sauf dans le cas particulier du couple et du torseur nul, où la résultante est nulle. Dans le cas d'un glisseur, les moments sur l'axe central sont nuls.

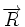
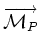
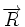
Pour le torseur cinématique d'un solide (dont les moments sont les vitesses des points du solide), la résultante est le vecteur instantané de rotation. Le mouvement du solide est en général la superposition d'un mouvement de rotation et d'un mouvement de translation parallèlement à l'axe de rotation instantané (vissage). Les points du solide en translation sont précisément les points de l'axe central du torseur cinématique.

Exemples

• Le champ des moments d'une force (ou de la somme de plusieurs forces) par rapport à un point est un torseur, dit torseur des actions mécaniques. La résultante du torseur est la somme des forces.

• Le champ des vitesses d'un solide indéformable en un instant donné est un torseur, appelé torseur cinématique du solide. La résultante est le vecteur instantané de rotation.

• Soit A un point affecté d'une masse m et d'une vitesse par rapport à un référentiel donné. Si l'on choisit un point P quelconque, on peut définir le torseur cinétique de A en P par :

. Ce torseur s'appelle le torseur cinétique de A. Sa résultante est la quantité de mouvement de A.

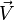
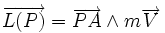
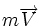
• On définit de même le torseur dynamique de A par le champ où est l'accélération de A. Si une force s'applique sur le point A, le principe fondamental de la dynamique énonce qu'il y a identité entre le torseur des forces et le torseur dynamique dans un référentiel galiléen (mécanique des solides).

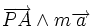
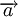
• Le champ de moments nuls s'appelle le torseur nul. Il correspond à un champ de forces dans le cas statique.

• Un couple est un champ vectoriel uniforme, donc représenté par un torseur dont la résultante est nulle. Physiquement, il correspond à un torseur de forces dont la résultante est nulle.

• Un glisseur est un torseur dont le champ des moments s'annule en au moins un point. Le torseur d'une force appliquée en un point est un glisseur, le moment étant nul sur la droite servant de support à la force. Le champ des vitesses d'un solide en rotation est un glisseur. La vitesse est nulle sur l'axe de rotation. Pour un glisseur, on peut utiliser la notation où désigne la résultante et O le point d'application où le moment est nul.

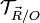
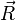
• Formulation du Principe d'Archimède :

Le torseur des forces de pression est égal et opposé au torseur des forces de gravité dans le fluide considéré.