Principe des puissances virtuelles - Définition

Genèse du principe

L'origine de ce principe revient à Jean Bernoulli, qui énonce en 1725 le principe des vitesses virtuelles, qui consiste à considérer la perturbation de l'équilibre d'un système mécanique par un mouvement infinitésimal respectant les conditions de liaison du système, un mouvement virtuel, et d'en déduire une égalité de puissance. Ce principe a été par la suite généralisé par D'Alembert et Lagrange en ce qui est connu actuellement sous le nom de principe de D'Alembert (1743).

Le principe des puissances virtuelles est une synthèse de ces principes, ancrée dans un cadre beaucoup plus rigoureux et mathématique (on parle alors de « dualisation » et non plus de « perturbation » de l'équilibre ou du mouvement par un mouvement infinitésimal).

Utilisation du PPV

• statique : calcul des forces internes dans les ossatures isostatiques.
• résolution de problèmes hyperstatiques.
• traitement des problèmes de stabilité de forme.
• calculs en régime dynamique.
• calcul élasto-plastique des ossatures métalliques.
• etc

Calculs avec des réducteurs

Le PPV : une démarche de modélisation

Le PPV constitue une démarche de modélisation : en effet, nous avons vu qu'il comporte deux « volets », l'un traduisant un équilibre de puissance, l'autre une nullité dans un type de mouvement. Parmi les trois types de puissances, il en existe deux dont les expressions sont relativement simples (même si elles font en réalité déjà intervenir des hypothèses et font donc déjà partie d'une modélisation) et une, celle des efforts intérieurs, qui pose un réel problème dès que l'on sort du cadre des systèmes de points matériels ou des solides indéformables.

Pour pouvoir appliquer le PPV, nous devons donc proposer une écriture pour la puissance des efforts intérieurs. Pour ce faire, il existe principalement deux démarches. La première consiste à changer d'échelle, à considérer un volume élémentaire de matière et à en déduire une expression des efforts intérieurs et donc de leur puissance. Nous allons présenter ici une autre démarche, qui permet d'aboutir à la théorie du premier gradient et aux théories de gradients d'ordres plus élevés.

Exemples de modélisation des milieux continus

Théorie du gradient d'ordre zéro

1. On suppose qu'il existe une densité volumique (ou massique) de puissance des efforts intérieurs, p_i telle que
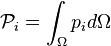
2. On suppose que cette densité volumique peut s'écrire où A est un champ de vecteur.

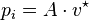
L'hypothèse 2. revient à représenter les efforts intérieurs par un champ de vecteur.

Soit le champ rigidifiant , d'après le PPV on a donc :

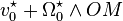
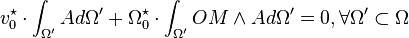
Ce qui conduit à A = 0

On vient de montrer que si l'on représente les efforts intérieurs par un champ de vecteur, ce champ est nécessairement nul.

Théorie des gradients

On peut remplacer l'hypothèse 2. par l'hypothèse suivante :

2'. la densité volumique de puissance des efforts intérieurs est une forme linéaire de faisant intervenir et ses gradients successifs.

Si l'on choisit de s'arrêter au premier gradient, on obtient la théorie du premier gradient, qui est la modélisation la plus courante pour un milieu continu, on peut alors montrer que les efforts intérieurs sont représentés par un tenseur d'ordre 2, , qui est symétrique et vérifie où n est le vecteur normal sortant à la frontière de Ω et F l'effort surfacique appliqué sur cette frontière.

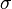
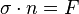
On peut prendre des gradients d'ordres plus élevés, ce qui conduit à des modèles plus complexes mais permettant de rendre compte d'effets plus subtils. Ainsi, avec le premier gradient, on ne peut pas couper une motte de beurre, et il faut monter au troisième gradient pour pouvoir la perforer.