Processus autorégressif - Définition
La liste des auteurs de cet article est disponible ici.
Processus AR(1)
Un processus autorégressif d'ordre 1 s'écrit:
Représentation en moyenne mobile
On peut formuler le processus AR(1) de manière récursive par rapport aux conditions précédentes:
En remontant aux valeurs initiales, on aboutit à:
Propriété —
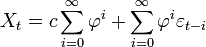
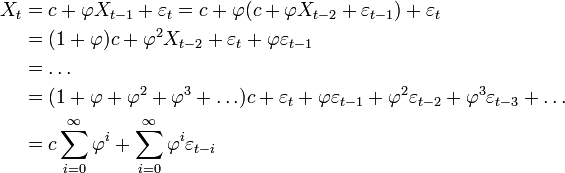
Il est à noter que les sommes vont ici jusqu'à l'infini. Cela est dû au fait que les séries temporelles sont souvent supposées commencer depuis
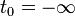
On peut voir que Xt est le bruit blanc convolé avec le noyau
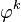
Représentation dans le domaine de la fréquence
La Densité spectrale de puissance est la Transformée de Fourier de la fonction d'autocovariance. Dans le cas discret, cela s'écrit:
Ce développement est périodique dû à la présence du terme en cosinus au dénominateur. En supposant que le temps d'échantillonnage (Δt = 1) est plus petit que le decay time (τ), alors on peut utiliser une approximation continue de Bn:
qui présente une forme lorentzienne pour la densité spectrale:
où γ = 1 / τ est la fréquence angulaire associée à τ.
Moments d'un processus AR(1)
Pour calculer les différents moments d'un processus AR(1), soit son espérance, sa variance, son autocovariance et son autocorrélation, on va supposer que les bruits blancs sont indépendamment et identiquement distribués, d'espérance nulle et de variance σ2 (que l'on note

Espérance
![\operatorname{E}[X_t]=\varphi^t X_0 + c\sum_{i=0}^{t-1}\varphi^i\,](https://static.techno-science.net/illustration/Definitions/autres/d/d56f66259ad9b7c7f595b7f758326454_23701ff6e294123dddeecbf0c42e5f9b.png)
Démonstration par raisonnement par récurrence
- P(0) (initialisation):
![\operatorname{E}[X_0] = X_0\,](https://static.techno-science.net/illustration/Definitions/autres/a/a0243479b391a1aff0e49d92dc8e9256_2e7b8408aebb5c9c4a9f3c7d85a8e4b2.png)
- P(t+1) (hérédité ):
Comme E est un opérateur linéaire:
Avec l'hypothèse d'induction:
Par un changement de variables dans la somme, i -> i-1:
Et, avec
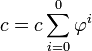
Variance
![\operatorname{Var}[X_t]= \sum_{i=0}^{\infty}\varphi^{2i}\sigma^2](https://static.techno-science.net/illustration/Definitions/autres/5/51eb5e19844e4d4e9395d21466a5813f_73fa8289e1f357ef0eb69b6f3d279309.png)
![\begin{align}\operatorname{Var}[X_t] &=\operatorname{E}\left [(X_t-\operatorname{E}[X_t])^2)\right ]\\ &=\operatorname{E}\left [(c\sum_{i=0}^{\infty}\varphi^i+\sum_{i=0}^{\infty}\varphi^i\varepsilon_{t-i}-c\sum_{i=0}^{\infty}\varphi^i)^2 \right ] \text{Selon resultat obtenu plus haut}\\ &=\operatorname{E} [(\sum_{i=0}^{\infty}\varphi^i\varepsilon_{t-i})^2 ]\\ &=\sum_{i=0}^{\infty}\varphi^{2i} \operatorname{E} [(\varepsilon_{t-i})^2 ]\quad \text{car }\operatorname{Var}(aX)=a^2\operatorname{Var}\\ &=\sum_{i=0}^{\infty}\varphi^{2i} \operatorname{Var} [\varepsilon_{t-i} ] \quad \text{car } \operatorname{Var}(X)=\operatorname{E}(X^2)-\operatorname{E}(X)^2 \quad \text{et } \operatorname{E}(X)=0 \quad \text{par hypothese}\\ &=\sum_{i=0}^{\infty}\varphi^{2i}\sigma^2 \end{align}](https://static.techno-science.net/illustration/Definitions/autres/5/5222da37f444919afb35257a333385b9_a6e9717101988750c12acee0220b009a.png)
Autocovariance
![\operatorname{Cov}[X_t,X_{t-j}]= \varphi^{j}\sum_{i=0}^{\infty}\varphi^{2i}\sigma^2](https://static.techno-science.net/illustration/Definitions/autres/a/aff9348c72728b770e495f7bd15649b3_139cf2bdca514c1ca9dd8e76c91ce2e5.png)
![\begin{align}\operatorname{Cov}[X_t,X_{t-j}] &=\operatorname{E}\left [(X_t-\operatorname{E}[X_t])(X_{t-j}-\operatorname{E}[X_{t-j}])\right ]\\ &=\operatorname{E}\left [(\sum_{i=0}^{\infty}\varphi^i\varepsilon_{t-i})(\sum_{i=0}^{\infty}\varphi^i\varepsilon_{t-i-j}) \right ]\\ &=\operatorname{E}[\sum_{i=0}^{\infty}\varphi^{2i}\varphi^{j}\varepsilon_{t-i}\varepsilon_{t-i-j} ]\\ &=\varphi^{j}\sum_{i=0}^{\infty}\varphi^{2i}\operatorname{E}[\varepsilon_{t-i}\varepsilon_{t-i-j} ]\\ &=\varphi^{j}\sum_{i=0}^{\infty}\varphi^{2i}\operatorname{E}[\varepsilon_{t-i}]\operatorname{E}[\varepsilon_{t-i-j}] \qquad \text{par hypothese d independance des } \varepsilon_{t-i}\\ &=\varphi^{j}\sum_{i=0}^{\infty}\varphi^{2i}\operatorname{E}[(\varepsilon_{t-i})^2]\\ &=\varphi^{j}\sum_{i=0}^{\infty}\varphi^{2i}\operatorname{Var}[\varepsilon_{t-i}] \qquad \text{voir resultat pour la variance}\\ &=\varphi^{j}\sum_{i=0}^{\infty}\varphi^{2i}\sigma^2 \end{align}](https://static.techno-science.net/illustration/Definitions/autres/7/76fe984a4a979a49d666e68b1fb5239a_a8cedc896037c483e162067fbe2e0739.png)
Autocorrélation
![\operatorname{Corr}[X_t,X_{t-j}]\equiv \frac{\operatorname{Cov}[X_t,X_{t-j}]}{\operatorname{Var}(X_t)}=\varphi^j](https://static.techno-science.net/illustration/Definitions/autres/3/3280cc2a4a6c986442b57e7b21cc32b8_9e7ac41ebfc466d1ae2a113c5d1e4f47.png)
Conditions de stationnarité
Le paramètre


ϕ<1
Les résultats suivant viennent du fait que si | q | < 1 alors la série géométrique
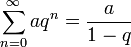
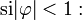
On peut voir que la fonction d'autocovariance décroît avec un taux de
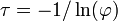
ϕ=1
Lorsque
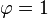
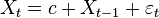
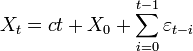
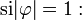
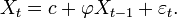
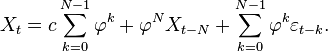
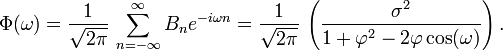
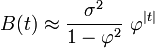
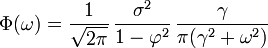
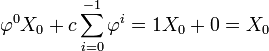
![\operatorname{E}[X_{t+1}]= \operatorname{E}[c + \varphi X_t + \epsilon_t]\,](https://static.techno-science.net/illustration/Definitions/autres/7/7901eb8061ff97e4f42a97af04515f53_fe119bfe9e5a8a27a11174a4767fe369.png)
![\operatorname{E}[X_{t+1}]= c + \varphi \operatorname{E}[X_t]\,](https://static.techno-science.net/illustration/Definitions/autres/2/21b08384deae4a65d3f39baea52442c6_8f6efcec51ec77a1642058af6c066584.png)
![\operatorname{E}[X_{t+1}]=c + \varphi (\varphi^t X_0 + c \sum_{i=0}^{t-1}\varphi^i)\,](https://static.techno-science.net/illustration/Definitions/autres/5/52127500ce166e193499fe26e518282b_a3a0ea991c8b037de8115c0b1e01ae19.png)
![\operatorname{E}[X_{t+1}]=c + \varphi^{t+1} X_0 + c \sum_{i=0}^{t-1}\varphi^{i+1}\,](https://static.techno-science.net/illustration/Definitions/autres/0/04c0c516ac7763b3a0cb50ad078bb68a_d2488b80eedd6c6332f96f315dfcd3d5.png)
![\operatorname{E}[X_{t+1}]= \varphi^{t+1} X_0 + c + c \sum_{i=1}^{t}\varphi^i\,](https://static.techno-science.net/illustration/Definitions/autres/a/ae13f888f98270b8898af1f02bc97440_730af99a95dad1a0efe79c2affd8d9d9.png)
![\operatorname{E}[X_{t+1}]= \varphi^{t+1} X_0 + c \sum_{i=0}^{t}\varphi^i\,](https://static.techno-science.net/illustration/Definitions/autres/5/5df3bc116927a5959ca07243310d65ee_6e60d7222b4903fd84cc618ef5a73499.png)
![\operatorname{E}[X_t]=\frac{c}{1-\varphi}](https://static.techno-science.net/illustration/Definitions/autres/2/2588d2037fe2912638edda7f3f5dde96_9528e84c6d6beef21aa8ab277b7bcea5.png)
![\operatorname{Var}[X_t]= \frac{\sigma^2}{1-\varphi^2}](https://static.techno-science.net/illustration/Definitions/autres/f/f8645dfe75034a6012d19a916c3c8e94_ce8e608eef848237b42ee8a120b9945a.png)
![\operatorname{Cov}[X_t,X_{t-j}]= \frac{\varphi^j}{1-\varphi^2} \sigma^2](https://static.techno-science.net/illustration/Definitions/autres/2/26fbddf2f60d475b5d8fccd3a479f587_8b3e2896bba5c0622bd1403a35dc5221.png)
![\operatorname{Corr}[X_t,X_{t-j}]=\varphi^j](https://static.techno-science.net/illustration/Definitions/autres/4/4bb64199414cf09107fe6e9f8d2963dc_3dedd8fc07957b595f8f7117eebb727e.png)
![\operatorname{E}[X_t]=ct+X_0\,](https://static.techno-science.net/illustration/Definitions/autres/a/a66354c85e727bf124458bb999a8edbe_1bd52e0a16a5d00ebfd7c564fb855902.png)
![\operatorname{Var}[X_t]= t\sigma^2\,](https://static.techno-science.net/illustration/Definitions/autres/6/6f6a4a5aabe6f22f49f77b406ca8bc88_7b4418e47acfde0bd0f4e807b17038da.png)
![\operatorname{Cov}[X_t,X_{t-j}]= (t-j)\sigma^2\,](https://static.techno-science.net/illustration/Definitions/autres/8/80ff730b72abedbf81dc0dd6c14e22cc_85fea5d6e19deb7f2a0357104df71643.png)