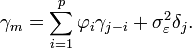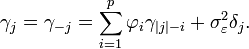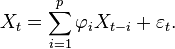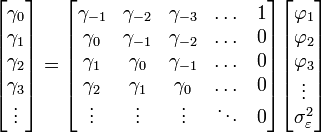Processus autorégressif - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Un processus autorégressif est un modèle de régression pour séries temporelles dans lequel la série est expliquée par ses valeurs passées plutôt que par d'autres variables.
Définition
Un processus autorégressif d'ordre p, noté AR(p) est donné par:
Définition — AR(p):
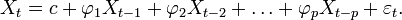
où
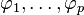
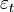
En utilisant L l'opérateur des retards, on peut l'écrire:
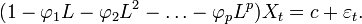
Processus AR(p)
Un processus AR(p) s'écrit:
Moments
Les différents moments d'un processus stationnaire (voir section suivante) sont:
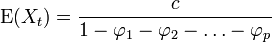
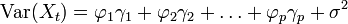
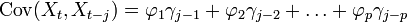
Les formules de la variance et de la covariance correspondent aux équations dites de Yule et walker (voir plus bas).
Condition de stationarité
Théorème — Un processus AR(p) est stationnaire si le module des solutions (les racines) de son équation caractéristique est à chaque fois strictement supérieur à 1 en valeur absolue.
La condition est souvent formulée différemment, selon laquelle les racines doivent être en dehors du cercle complexe unitaire.
Exemple: AR(1)
Le polynôme des retards d'un processus AR(1)
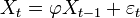
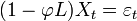
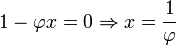

Exemple: AR(2)
Le polynôme des retards d'un processus AR(2)
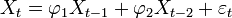
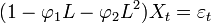
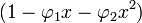
Équations de Yule-Walker
Les équations de Yule-Walker établissent une correspondance directe entre les paramètres du modèle (les

équation YW —
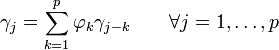
- Les coefficients γj représentent la fonction d'autocovariance de X d'ordre j.
Lorsque l'on inclut également l'autocovariance d'ordre 0 (en fait la variance), il faut également rajouter la variance des résidus pour la première équation. Ce terme supplémentaire ne se retrouve que dans la première équation car on a fait l'hypothèse d'indépendance des résidus (et donc
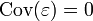
équation YW —
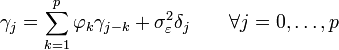
-
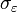
Il est aussi possible d'exprimer ces équations en fonctions de l'autocorrélation:
équation YW —
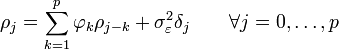
Exemples
AR(1)
Pour un processus AR(1), on a que:
On remarque que l'on retrouve rapidement, avec j=1, le résultat obtenu plus haut que:
- -
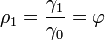
- -
![\operatorname{Var}[X_t]= \frac{\sigma^2}{1-\varphi^2}](https://static.techno-science.net/illustration/Definitions/autres/f/f8645dfe75034a6012d19a916c3c8e94_ce8e608eef848237b42ee8a120b9945a.png)
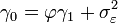
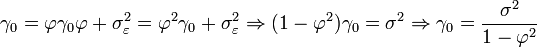
AR(p)
Que l'on peut écrire sous forme matricielle:
Preuve
L'équation définissante du processus AR est
En multipliant les deux membres par Xt − m et en prenant l'espérance, on obtient
Or, il se trouve que E[XtXt − j] = γj par définition de la fonction d'autocovariance. Les termes du bruit blancs sont indépendants les uns des autres et, de plus, Xt − j est indépendant de εt où j est plus grand que zéro. Pour j > 0, E[εtXt − j] = 0. Pour j = 0,
Maintenant, on a pour j ≥ 0,
Par ailleurs,
qui donne les équations de Yule-Walker:
pour j ≥ 0. Pour j < 0,
Estimation
En partant du modèle AR(p) sans constante donné par:
Les paramètres à estimer sont les
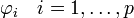
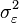
Méthode de Yule-Walker
La méthode consiste à reprendre les équations de Yule-Walker en inversant les relations: on exprime les coefficients en fonction des autocovariances. On applique alors le raisonnement de la Méthode des moments: on trouve les paramètres estimés d'après les autocovariances estimées.
En prenant l'équation sous sa forme matricielle:
Le vecteur des paramètres
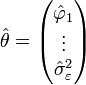
Maximum de vraisemblance inconditionnel
L'estimation d'un modèle AR(P) par la méthode du maximum de vraisemblance est délicate car la fonction de vraisemblance est très complexe et n'a pas de dérivée analytique. Cette difficutlé provient de l'interdépendance des valeurs, ainsi que du fait que les observations antérieures ne sont pasd toutes disponibles pour les p premières valeurs.
Maximum de vraisemblance conditionnel
Une manière de simplifier la complexité de la fonction de vraisemblance est de conditionner cette fonction aux p premières observations. La fonction de log-vraisemblance devient:
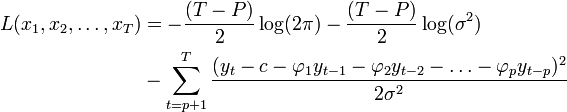
La maximisation de cette fonction par rapport aux paramètres

L'estimateur obtenu sera équivalent à l'estimateur inconditionnel dans de grands échantillons et tous deux ont la même distribution asymptotique (Hamilton 1994, p. 126). Il peut être biaisé
Propriétés des estimateurs
Davidson et McKinnon (1993) rapportent que l'estimateur des moindres carrés conditionnel est biaisé, mais néanmoins convergent. Cryer et Chan (2008) proposent une simulation Monte-Carlo pour tester les différents estimateurs.
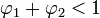
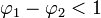
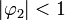

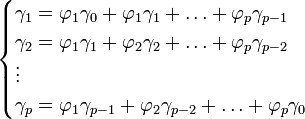
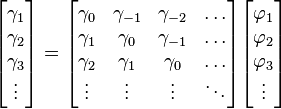
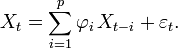
![E[X_t X_{t-j}] = E\left[\sum_{i=1}^p \varphi_i\,X_{t-i} X_{t-j}\right]+ E[\varepsilon_t X_{t-j}].](https://static.techno-science.net/illustration/Definitions/autres/e/ee31891b6625fdc5868e9550ac11d6ff_e8234b9eadff296d61f2f144a56047ea.png)
![E[\varepsilon_t X_{t}] = E\left[\varepsilon_t \left(\sum_{i=1}^p \varphi_i\,X_{t-i}+ \varepsilon_t\right)\right] = \sum_{i=1}^p \varphi_i\, E[\varepsilon_t\,X_{t-i}] + E[\varepsilon_t^2] = 0 + \sigma_\varepsilon^2,](https://static.techno-science.net/illustration/Definitions/autres/8/88d3b15dfb38be4b18970c036c4348d1_ba572d8814d88ee5d5ef5e3be78657a5.png)
![\gamma_j = E\left[\sum_{i=1}^p \varphi_i\,X_{t-i} X_{t-j}\right] + \sigma_\varepsilon^2 \delta_j.](https://static.techno-science.net/illustration/Definitions/autres/3/3f757aa9c24969cdad8ea62e02aa4355_11f3e5353c8c2bab2f4031bb63d983d5.png)
![E\left[\sum_{i=1}^p \varphi_i\,X_{t-i} X_{t-j}\right] = \sum_{i=1}^p \varphi_i\,E[X_{t} X_{t-j+i}] = \sum_{i=1}^p \varphi_i\,\gamma_{j-i},](https://static.techno-science.net/illustration/Definitions/autres/9/9e1c6dc672ae98ee6e72d1cffb91289e_8fdf83838f6fadc9fc609a9cfb21b6de.png)