Processus de Markov - Définition

Introduction

En mathématiques, un processus de Markov est un processus stochastique possédant la propriété de Markov. Dans un tel processus, la prédiction du futur à partir du présent n'est pas rendue plus précise par des éléments d'information concernant le passé. Les processus de Markov portent le nom de leur découvreur, Andreï Markov.

Un processus de Markov en temps discret est une séquence de variables aléatoires. L'ensemble de leurs valeurs possibles est appelé l’espace d'états, la valeur étant l'état du processus à l'instant Selon les auteurs, le vocable « chaîne de Markov » désigne les processus de Markov à temps discret ou uniquement les processus de Markov à temps discret et à espace d'états discret, i.e. les processus de Markov à temps discret dont l'espace d'états est fini ou dénombrable.

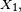
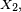
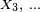
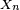
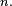
Si la loi conditionnelle de sachant le passé, i.e. sachant est une fonction de seul, alors :

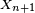
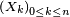
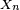
où x est un état quelconque du processus. L'identité ci-dessus identifie la probabilité markovienne.

Andreï Markov a publié les premiers résultats de ces processus en 1906.

Une généralisation à un espace d'états infini dénombrable a été donnée par Kolmogorov en 1936.

Les processus de Markov sont liées au mouvement brownien et à l'hypothèse ergodique, deux sujets de physique statistique qui ont été très importants au début du XX^e siècle.

Types de processus de Markov

Espace d'états discret

Lorsque les variables aléatoires successives sont des variables discrètes munies d'une fonction de probabilité, on parle de chaîne de Markov.

Bien que les chaînes de Markov s'appliquent à des phénomènes dont l'aspect temporel est généralement sans intérêt, on peut associer aux valeurs successives les instants . La propriété markovienne selon laquelle la probabilité d'un état du système ne dépend que de son état précédent à travers une probabilité conditionnelle appelée probabilité de transition s'exprime par :

.

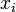
Une chaîne de Markov est entièrement définie par la probabilité au premier ordre et la probabilité de transition. On obtient par exemple la probabilité au second ordre par :

.

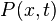
Elle est donc également définie par la probabilité au second ordre. Enfin, elle peut être définie par l'état initial et la probabilité de transition.

Espace d'états continu

Les chaînes de Markov trouvent des applications dans les domaines les plus divers mais les processus considérés dans les problèmes dynamiques, en particulier en vibrations, portent généralement sur des variables aléatoires continues.

Dans ces conditions, la probabilité d'obtenir une valeur donnée est généralement nulle et les probabilités d'apparition doivent être remplacées par des densités de probabilité dans la formule de la propriété markovienne :

Temps discret et temps continu

Les considérations qui précèdent restent valables si les intervalles de temps deviennent infiniment petits. Cette remarque est particulièrement intéressante dans le cas d'une équation différentielle. Si elle est du premier ordre, la mise en différences finies fait apparaître un mécanisme markovien. Pour les ordres supérieurs et les systèmes différentiels, la décomposition en équations du premier ordre conduit à un système markovien à plusieurs dimensions.