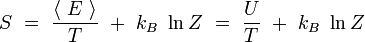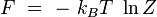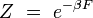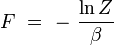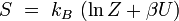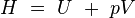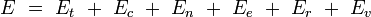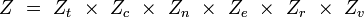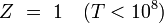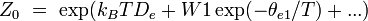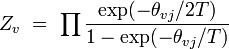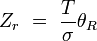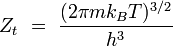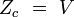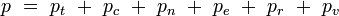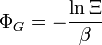Physique statistique - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La physique statistique a pour but d'expliquer le comportement et l'évolution de systèmes physiques comportant un grand nombre de particules (on parle de systèmes macroscopiques), à partir des caractéristiques de leurs constituants microscopiques (les particules). Ces constituants peuvent être des atomes, des molécules, des ions, des électrons, des photons, des neutrinos, ou des particules élémentaires. Ces constituants, et les interactions qu'ils peuvent avoir entre eux, sont en général décrits par la mécanique quantique, mais la description macroscopique d'un ensemble de tels constituants ne fait, elle, pas directement appel (ou en tout cas pas toujours) à la mécanique quantique. De fait, cette description macroscopique, en particulier la thermodynamique, a été obtenue pour partie avant le développement de la mécanique quantique en tant que théorie physique, essentiellement dans la seconde moitié du XIXe siècle.
On distingue la physique statistique d'équilibre (au sens d'équilibre thermodynamique), auquel cet article est consacré, de la physique statistique hors d'équilibre.
Historique
La physique statistique (appelé aussi « thermodynamique statistique ») fut introduite initialement sous la forme de la théorie cinétique des gaz à partir du milieu du XIXe siècle, principalement par Kelvin, Maxwell et Boltzmann. Cette première approche visait à proposer un modèle simple de la matière à l'échelle atomique, et en particulier des collisions entre atomes ou molécules, pour reproduire le comportement de certaines quantités macroscopiques. C'est à cette époque que l'interprétation de la pression comme mesure de la quantité de mouvement des constituants d'un gaz a été formalisée.
La mécanique statistique fut formalisée en 1902 par Gibbs, son formalisme permettant de généraliser et de justifier a posteriori les principes de la thermodynamique d'équilibre.
Les premières extensions de la physique statistique, par rapport à la mécanique statistique, ont été l'introduction des propriétés électriques et magnétiques de la matière au sein des modèles, permettant la description des transitions de phase dans les matériaux magnétiques ou diélectriques, comme la transition ferromagnétique.
Une autre étape importante fut la modification des formules statistiques, entre les années 1920 et 1930, pour tenir compte des effets de l'indiscernabilité au niveau quantique des particules (principe d'exclusion de Pauli). Cette modification fut effectuée par Bose et Einstein pour les systèmes de particules de spin entier (bosons) et par Fermi et Dirac pour les systèmes de particules de spin demi-entier (fermions).
Outils et procédés
La formulation moderne de cette théorie se fonde sur la description des systèmes physiques étudiés par le biais d'ensembles statistiques. De tels ensembles représentent la totalité des configurations possibles du système associées à leur probabilités de réalisation. À chaque ensemble est associée une fonction de partition qui, par manipulations mathématiques, permet d'extraire les grandeurs thermodynamiques du système. Selon les relations du système avec le reste de l'univers, on distingue généralement trois types d'ensemble, du plus simple au plus complexe :
- l'ensemble microcanonique
- l'ensemble canonique
- l'ensemble grand canonique
| Tableau résumant les ensembles en physique statistique | Ensembles | ||
| Microcanonique | Canonique | Grand-canonique | |
| Variables indépendantes | E, N, V ou B | T, N, V ou B | T, μ, V ou B |
| Fonction microscopique | Ω | ||
| Potentiel thermodynamique | |||
Ensemble microcanonique
Cet ensemble décrit le cas idéal d'un système complètement isolé d'énergie E constante, et n'échangeant donc ni particule, ni énergie, ni volume avec le reste de l'univers. L'intérêt de ce modèle est qu'il permet de définir l'entropie sous sa forme la plus simple.
Entropie microcanonique
Le système étant à l'équilibre macroscopique, mais libre d'évoluer à l'échelle microscopique entre Ω micro-états différents, son entropie est donnée par la formule de Boltzmann (1877) :
|
|
où kB est la constante de Boltzmann. Cette définition correspond à l'entropie de Shannon :
|
|
d'une configuration de Ω micro-états équiprobables :
|
|
Extensivité de l'entropie
L'énergie macroscopique totale E du système isolé étudié est toujours supérieure ou égale à une certaine valeur E0 minimale, appelée énergie de l'état fondamental du système. De plus, le comptage du nombre Ω de micro-états du système fermé d'énergie totale E nécessite en général l'introduction d'une certaine incertitude ΔE d'ordre mésoscopique.
On peut montrer que, pour un système « ordinaire », le nombre Ω de micro-états est une fonction rapidement croissante de l'énergie de la forme :
|
|
où N le nombre de degrés de liberté total du système, supposé très grand. Il est alors possible de montrer que lorsque l'énergie totale E n'est pas trop proche de sa valeur minimale, l'entropie S(E,N) calculée par la formule de Boltzmann est :
- de l'ordre de N, donc l'entropie microcanonique est bien extensive à la limite thermodynamique.
- indépendante de la valeur exacte de l'incertitude ΔE.
Ensemble canonique
L'ensemble canonique décrit un système fermé en équilibre thermique avec un thermostat extérieur. Ce système fermé peut donc échanger de l'énergie sous forme de transfert thermique avec l'extérieur, à l'exclusion de toute autre quantité.
Fonction de partition canonique
Dans les conditions citées ci-dessus, on démontre que la probabilité pi pour que le système fermé réalise un état i d'énergie Ei est donnée par la formule de Boltzmann :
|
|
où le facteur
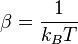
|
|
Z est appelé la fonction de partition canonique du système fermé, et s'écrit explicitement :
|
|
Cette fonction de partition permet de déduire toutes les grandeurs macroscopiques du système fermé comme moyennes des grandeurs microscopiques associées.
Observables macroscopiques
L'énergie interne U est la moyenne macroscopique de l'ensemble des énergies microscopiques Ei :
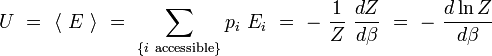
|
De même, pour toute grandeur A prenant des valeurs Ai définies sur les micro-états i associés aux énergies Ei, on peut définir la valeur moyenne :
|
|
Appliquons en particulier cette formule à l'entropie, en posant que les micro-états Ei définissent des systèmes représentables comme des ensembles microcanoniques, nous avons défini pour chaque micro-état i une entropie microcanonique :
|
|
L'entropie totale du système prend alors la forme :
|
|
|
|
Remplaçons la probabilité par son expression dans le logarithme :
|
|
|
|
D'après la définition de la température inverse, on a : kBβ = 1 / T, d'où :
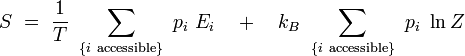
|
On reconnaît dans le premier terme la valeur moyenne de l'énergie. Par ailleurs, le logarithme de Z est indépendant de l'indice i. On obtient alors en utilisant la condition de normalisation des probabilités :
|
|
En rapprochant cette formule de celle donnant l'énergie libre F en thermodynamique : F = U - T S, il vient naturellement :
|
|
ou encore :
|
|
Tableau récapitulatif
Les expressions de F, de U et de S sont suffisantes pour en déduire toutes les autres grandeurs thermodynamiques :
| Nom | Formule |
| énergie libre de Helmholz |
|
| énergie interne |
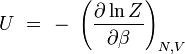
|
| pression |
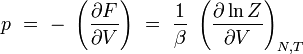
|
| entropie |
|
| enthalpie libre de Gibbs |
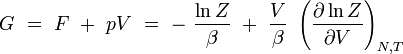
|
| enthalpie |
|
| chaleur spécifique à volume constant |
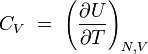
|
| chaleur spécifique à pression constante |
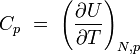
|
| potentiel chimique |
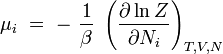
|
Pour la dernière entrée, il ne s'agit pas de l'ensemble grand-canonique. Il est souvent utile de considérer que l'énergie d'une molécule donnée est distribuée entre plusieurs modes. Par exemple, l'énergie de translation est la partie de l'énergie relative au mouvement du centre de masse de la molécule. L'énergie de configuration se rapporte à la portion de l'énergie associée aux diverses forces attractives et répulsives entre les molécules du système. Les autres modes sont tous considérés comme internes aux molécules. Ils incluent les modes rotationnels, vibrationnels, électroniques et nucléaires. Si nous supposons que chaque mode est indépendant, l'énergie totale peut être exprimée comme la somme de la contribution de chaque composant :
|
|
où les indices t, c, n, e, r et v correspondent aux énergies des modes de translation, de configuration, nucléaires, électroniques, rotationnels, et vibrationnels respectivement.
En substituant cette équation dans la toute première équation, nous obtenons :
![Z \ = \ \sum_{ i_j \ \mathrm{niveau \ interne \ a} \ j } \ \left[ \ \prod_{j \, \in \, \{ \, t,c,n,e,r,v \, \}} \ \exp \ ( \, - \, \beta \, E_{ji_j}) \ \right]](https://static.techno-science.net/illustration/Definitions/autres/d/d0a1da3db4885b5b94eb94e875f19850_07a53e7f9bab2bf69988c996da3486b7.png)
|
Grâce à l'indépendance des modes, on peut permuter la somme et le produit :
![Z \ = \ \prod_{j \, \in \, \{ \, t,c,n,e,r,v \, \}} \ \left[ \ \sum_{ i_j \ \mathrm{niveau \ interne \ a} \ j} \ \exp \ ( \, - \, \beta \, E_{ji_j}) \ \right]](https://static.techno-science.net/illustration/Definitions/autres/0/01193aee3d7558fd1552478d71dbbec7_aa173f32085d7ee0646af0d2ad89dba8.png)
|
Ainsi, pour chaque mode, on peut définir une fonction de partition associée, et on obtient la fonction de partition totale comme produit de ces fonctions de partition de modes :
|
|
Des expressions simples en sont dérivées pour chacun des modes relatifs à des propriétés moléculaires, telles que les fréquences rotationnelles et vibrationnelles. Les expressions des diverses fonctions de partitions sont données dans la table suivante :
| Type | Formule |
| nucléaire |
|
| électronique |
|
| vibrationnel |
|
| rotationnel(linéaire) |
|
| rotationnel (non linéaire) |
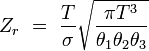
|
| translation |
|
| configuration (gaz parfait) |
|
Ces équations peuvent être combinées avec celles de la première table pour déterminer la contribution d'un mode énergétique spécifique aux propriétés thermodynamiques. Par exemple, la « pression de rotation » peut être déterminée de cette manière. La pression totale peut être trouvée en sommant les contributions de pression de tous les modes individuels :
|
|
Ensemble grand-canonique
Si le système est ouvert (c'est-à-dire s'il permet l'échange de particules avec l'extérieur), nous devons introduire les potentiels chimiques et remplacer la fonction de partition canonique par la fonction de partition grand-canonique :
![\Xi (V,T,\mu)=\sum_i \exp \left(\beta[\sum_{j=1} ^n \mu_j N_{ij}-E_i]\right) \,](https://static.techno-science.net/illustration/Definitions/autres/8/8c281b28d229ebd89cd8b96ea193521e_18d973f706ca1f05f4f081223002ca14.png)
|
où Nij est le nombre de particules de la j-ème espèce dans la i-ème configuration. Il peut arriver aussi que nous ayons d'autres variables à ajouter à la fonction de partition, une variable par quantité conservée. La plupart d'entre elles, cependant, peuvent sans problème être interprétées comme des potentiels chimiques. Dans la plupart des problèmes de matière condensée, les effets sont non relativistes et la masse est conservée. La masse est inversement reliée à la densité, qui est la variable conjuguée de la pression.
Dans le reste de l'article, nous ignorerons cette difficulté et supposerons que les potentiels chimiques ne changent rien. Examinons l'ensemble grand canonique.
Recalculons toutes les expressions en utilisant l'ensemble grand-canonique. Le volume est fixé et ne figure pas dans ce traitement. Comme précédemment, j est l'indice des particules de la j-ème espèce et i est l'indice du i-ème micro-état :
![U=\sum_i {E_i \exp \left(-\beta[E_i-\sum_{j=1} \mu_j N_{ij}]\right) \over \Xi}\,](https://static.techno-science.net/illustration/Definitions/autres/a/a109bc707aa018beeef51730dee3a973_a6a0c6541a9ff783b0e774e718923ad1.png)
![N_j=\sum_i {N_{ij} \exp \left(-\beta[E_i-\sum_{j=1} \mu_j N_{ij}]\right) \over \Xi}\,](https://static.techno-science.net/illustration/Definitions/autres/a/a6d786f6bfdeb727d45b9a1686eae979_8cd9a30bff1278ae203bc5393589aaf0.png)
|
| Nom | Formule |
| Grand potentiel |
|
| énergie interne |
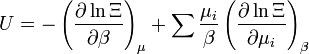
|
| nombre de particules |
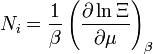
|
| entropie |
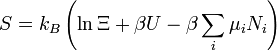
|
| énergie libre de Helmholtz |
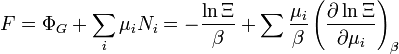
|
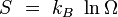
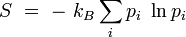
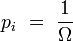
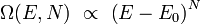
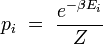
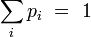

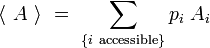
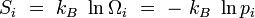
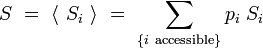

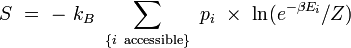
![= \ + \ k_B \ \sum_{\{i \ \mathrm{accessible} \}} \ p_i \ \times \ \left[ \ \beta E_i + \ln Z \ \right]](https://static.techno-science.net/illustration/Definitions/autres/3/3d48aac34bfc6f37c0174a4e63a272b9_85ae0e05ba310ed49a2980f7b9441711.png)