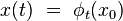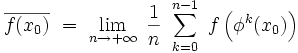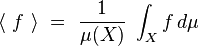Hypothèse ergodique - Définition

Introduction

L'hypothèse ergodique, ou hypothèse d'ergodicité, est une hypothèse fondamentale de la physique statistique. Elle fut formulée initialement par Ludwig Boltzmann en 1871 pour les besoins de sa théorie cinétique des gaz. Elle s'appliquait alors aux systèmes composés d'un très grand nombre de particules, et affirmait qu'à l'équilibre, la valeur moyenne d'une grandeur calculée de manière statistique est égale à la moyenne d'un très grand nombre de mesures prises dans le temps. La première valeur est celle que permet de calculer la physique statistique, la seconde est proche de ce qu'on peut expérimentalement mesurer. L'hypothèse ergodique est donc fondamentale pour un bon rapprochement entre la théorie et l'expérience.

Un système pour lequel l'hypothèse ergodique est vérifiée sera qualifié de système ergodique. Dans la plupart des cas, il est très difficile de démontrer rigoureusement si un système est ergodique ou non. L'analyse mathématique de ce problème a donné naissance à la théorie ergodique qui précise la nature mathématique de l'hypothèse et donne des résultats sur ses conditions de validité. Mais l'hypothèse ergodique reste souvent une simple hypothèse, jugée vraisemblable a posteriori quand elle permet de faire des prédictions correctes. En ce sens, elle constitue un point faible de la physique statistique.

L'hypothèse d'ergodicité intervient également en traitement du signal, où elle consiste à admettre que l'évolution d'un signal aléatoire au cours du temps apporte la même information qu'un ensemble de réalisations. Elle est importante dans l'étude des chaînes de Markov, les processus stationnaires et pour l'apprentissage numérique.

Formalisation mathématique de l'hypothèse

Représentation d'un système dans l'espace des phases

Soit un système à N degrés de liberté décrits à l'instant t par :

• les N coordonnées généralisées qⁱ(t), (i = 1,...,N)

• les N moments conjugués p_j(t), (j = 1,...,N).

À chaque instant, les 2N coordonnées (qⁱ(t),p_j(t)) définissent un point x(t) dans l'espace des phases, qui représente l'état du système à cet instant t.

On considère de plus que le système est à l'équilibre, c'est-à-dire que ses propriétés sont invariantes dans le temps. Un tel système satisfait toujours à la conservation de l'énergie qui s'écrit :

de telle sorte que sa dynamique est en fait toujours restreinte à une hypersurface à 2N − 1 dimensions. On supposera dans la suite que le système hamiltonien considéré est invariant par translation dans le temps et qu'il ne possède pas d'autre constante du mouvement que l'énergie.

Évolution du système, flot hamiltonien

L'évolution dynamique du système selon les équations canoniques de Hamilton à partir d'une condition initiale engendre le flot hamiltonien , c'est-à-dire le groupe continu à un paramètre tel que :

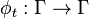
La succession des positions x(t) dans l'espace des phases se traduit par une courbe continue, appelée orbite.

Grandeurs mesurables et valeurs moyennes

A une grandeur physique mesurable correspond une fonction sur l'espace des phases qui à chaque point, correspondant à un état du système, associe une valeur. On notera f cette fonction. Il existe deux valeurs moyennes distinctes pour cette grandeur. On peut faire une moyenne temporelle en faisant la moyenne d'une série de mesures effectuées sur un temps suffisamment long. Mathématiquement on la représente par la limite (si elle existe) :

Cette valeur moyenne dépend a priori de la condition initiale x₀.

On peut également définir la moyenne d'ensemble de f, ou moyenne microcanonique, par :

La moyenne spatiale et la moyenne temporelle n'ont a priori pas de raison d'être égales. L'hypothèse ergodique consiste à supposer qu'elles le sont.

Le théorème ergodique de Birkhoff

L'évolution du système dans le temps est déterminé par le flot hamiltonien, c'est-à-dire l'application φ. Cette application sera dite ergodique pour une mesure donnée si et seulement si tout ensemble mesurable invariant sous φ est de mesure nulle, ou de complémentaire de mesure nulle.

Le théorème de Birkhoff montre alors que lorsque l'application φ est ergodique, moyenne spatiale et moyenne temporelle sont effectivement égales presque partout.

Les hypothèses ergodiques forte et faible

Le théorème de Birkhoff présenté ci-dessus permet de formuler l'hypothèse ergodique non plus comme une égalité de moyenne, mais en fonction des propriétés du flot hamiltonien φ, c'est-à-dire de l'évolution du point représentatif du système dans l'espace des phases.

On peut alors distinguer deux hypothèses ergodiques distinctes :

Un système hamiltonien invariant par translation dans le temps sera dit ergodique au sens fort si le point représentatif de ce système passe au cours du temps par chaque point de l'hypersurface d'énergie constante.

Un système hamiltonien invariant par translation dans le temps sera dit ergodique au sens faible si le point représentatif de ce système passe au cours du temps aussi près que l'on veut de chaque point de l'hypersurface d'énergie constante.

Boltzmann et Maxwell utilisèrent dans leurs travaux les deux énoncés de façon indifférenciée. La non-équivalence mathématique des deux hypothèses ergodiques précédentes n'a été reconnue explicitement qu'en 1910 par Paul Hertz.