Propriété de Markov - Définition
La liste des auteurs de cet article est disponible ici.
Propriété de Markov faible (temps continu, espace discret)
Mathématiquement, si X(t), t > 0, est un processus stochastique, et si x(t), t > 0, est une fonction, la propriété de Markov est définie ainsi :
Généralement, on utilise une hypothèse d'homogénéité dans le temps, c'est-à-dire :
Dans certains cas, un processus à première vue non-markovien peut tout de même avoir des représentations markoviennes en modifiant le concept d'état actuel et futur. Soient X un intervalle de temps, et Y un processus tel que chaque état de Y représente un intervalle de temps de X :
Si Y est markovien, alors c'est la représentation markovienne de X et X qui est alors appelée processus de Markov du second ordre. Les processus d'ordre supérieur sont définis de la même manière.
Propriété de Markov forte (temps discret, espace discret)
Temps d'arrêt
Notons
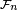
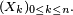
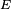
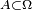
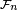
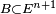
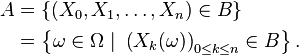
Définition — Une variable aléatoire
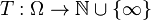
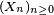
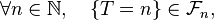
ou bien, équivalemment, si,
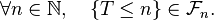
Interprétation. Imaginons que les variables aléatoires
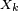
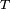
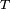

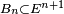
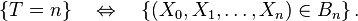
Cela interdit au joueur de prendre sa décision en fonction des résultats des parties futures : cela revient à faire l'hypothèse que don de double vue et tricherie sont exclus.
Pour une définition d'un temps d'arrêt en situation générale on pourra regarder
Les variables aléatoires ci-dessous sont des temps d'arrêt :
- Soit
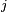
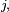
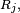

- On arrête donc de jouer dès qu'on arrive à l'état
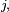
 par
par
- De même pour
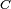
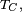
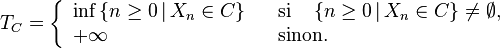
- L'instant de

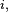
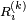

ou encore l'instant de

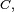
Pour

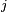
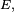
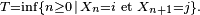
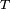
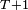
Définition et propriété — Soit
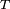
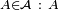
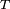
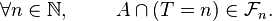
L'ensemble des évènements antérieurs à
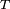

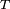
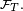
Interprétation. On sait que pour tout

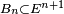
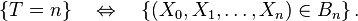
Si de plus
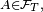

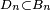
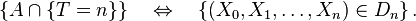
En quelque sorte, on teste si l'évènement
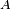
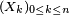
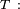
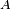
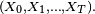
Propriété de Markov forte
Dans l'énoncé général de la propriété de Markov faible, l'instant « présent », n, peut-être remplacé par un instant « présent » aléatoire,
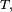
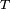
Propriété de Markov forte — Pour un temps d'arrêt
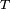
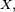
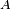
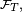
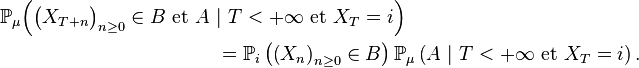
Cela peut s'interpréter comme une forme d'indépendance (une indépendance conditionnelle ) entre le passé,
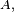
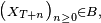
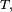
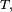
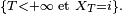
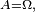
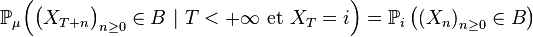
puis, en revenant à un élément général
Indépendance conditionnelle — Pour un temps d'arrêt
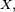
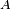
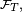
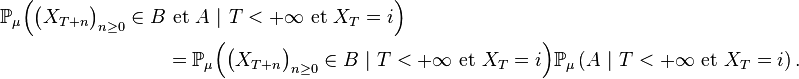
Cas particulier des temps de retour
Dans le cas où la chaîne de Markov est irréductible, où l'état

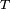
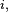
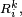
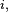
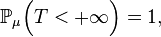
et que, par définition de
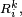
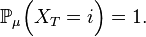
Ainsi les conditions apparaissant dans la propriété de Markov forte sont presque certaines. Or, dès que
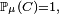
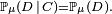
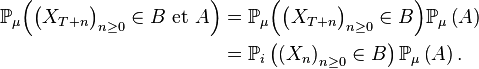
Pour tout k, il y a donc indépendance ( inconditionnelle ) entre les évènements qui précèdent le k-ème passage en


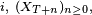

Les morceaux de trajectoires entre deux régénérations consécutives forment alors une suite de variables aléatoires i.i.d. (sauf le premier morceau, indépendant, mais éventuellement de loi différente, si la chaîne de Markov ne part pas de

![\mathrm{P}\big[X(t+h) = y \,|\, X(s) = x(s), s \leq t\big] = \mathrm{P}\big[X(t+h) = y \,|\, X(t) = x(t)\big], \quad \forall h > 0.](https://upload.wikimedia.org/math/3/2/8/328cf81e7a60bad9cfc2aee7014c2496.png)
![\mathrm{P}\big[X(t+h) = y \,|\, X(t) = x(t)\big] = \mathrm{P}\big[X(h) = y \,|\, X(0) = x(0)\big], \quad \forall t, h > 0.](https://upload.wikimedia.org/math/6/7/7/6770d1d628e3c9603fd1afe40e56dad8.png)
![Y(t) = \big\{ X(s) : s \in [a(t), b(t)] \, \big\}.](https://static.techno-science.net/illustration/Definitions/autres/2/252498d7ff02e909247c6084f75933a2_38f111c3e33fa58c4b0197607eb6777b.png)

















































