Puits de potentiel - Définition

Détermination de h(s) grâce à l'observation de T(H)

Cela s'appelle résoudre un problème inverse. Landau et Lifschitz (mécanique, ed Mir) traite ce problème difficile.

La notion mathématique qui s'applique bien ici est la notion de dérivée fractionnaire d'ordre 1/2, dite d'Abel. En fait c'est la fonction réciproque s(h) que l'on détermine {on a déjà vu dans le cas du pendule simple que h (et non s) est la bonne fonction inconnue, et alors on en déduit s(h(t))} : la formule est :

,

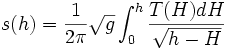
dont on vérifie immédiatement l'homogénéité s = sqrt(gHo)To. Voir ci-dessous la démonstration.

Expérimentation

Ayant récupéré la courbe T(H) expérimentalement, il n'est pas trop difficile sur une calculette de programmer la courbe précédente s(h). C'est en principe ce qui termine un Travail Pratique expérimental. Le soin à apporter au tracé de T(H) n'est pas trop crucial, mais on a parfois des surprises !

Quelques vérifications de cas connus

• la cuvette de Torricelli (cf diagramme horaire) avec T = 4sqrt(2H/gsinα: s= h/sinα.
• la cycloïde isochrone : s(h) telle que s^2(h) = 16 a h
• et aussi toutes les cuvettes de potentiel en V(x) = x^k , qui satisfont automatiquement au théorème du viriel, dont
  • le mouvement de Kepler : T² =a³ = 1/(-E)³ , qui donne bien U ~ -1/|s|.
  • si on rajoute la barrière centrifuge, la cuvette est non symétrique, mais le raisonnement (adapté) donne bien, quel que soit le moment cinétique, le résultat, U ~ -1/r.
• la cuvette h = Ho tan²(s/a) qui donne : gT² : = 4π².a²/(Ho+H).

Démonstration de la formule

La primitive fractionnaire 1/2 de la dérivée f'(x) est la dérivée 1/2 de f(x) (Théorème de réciprocité d'Abel) ;

mais on peut opter pour une démonstration sans l'artillerie lourde (des dérivées fractionnaires!)  ; voici celle empruntée à Landau (on a pris g=1) :

• remarquer que

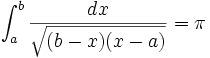
(penser à HM² = HA.HB, dans le triangle-rectangle AMB, inscrit dans le demi-cercle de diamètre AB : alors dx/HM = dφ ; d'où la réponse).

• remarquer que T(H) s'écrit , et donc

• ,

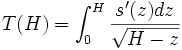
soit en intégrant sur la nouvelle variable H, de 0 à h, puis en intervertissant l'ordre d'intégration, d'abord en H, puis en z, l'obtention de la formule de réciprocité d'Abel.

On pourra s'exercer avec les résultats précédents.

Formule de perturbation

Très souvent en physique, le puits de potentiel est légèrement perturbé par l'adjonction d'un paramètre que l'on peut contrôler (champ magnétique : effet Zeeman classique ; champ électrique : effet Stark classique, etc.). Il est alors intéressant de savoir quelle est la nouvelle période T(H).

La règle est la suivante :

• soit le mouvement non perturbé s(t,H), de période T(H). Dans le plan de phase, l'orbite fermée, d'énergie H est décrite dans le sens rétrograde avec la période T(H) en enserrant une aire I(H)(en joule.seconde), appelée l'Action I(H). Un résultat classique de mécanique hamiltonienne est T(H) = dI/dH.
• Soit le nouveau potentiel V(x) + k .V₁(x), où k est un réel sans dimension très petit.
• soit k.I₁(H) la petite action (en joule.seconde)= T(H).[moyenne temporelle de k V₁(x)].
• La variation de période T1(H) est :

.

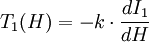
• si on veut le deuxième ordre, en k², il faudra rajouter :

+ (1/2!).k². avec I₂ (en joule².seconde) = T(H).[moyenne temporelle de V₁²(x)] ; etc.

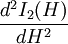
Application: la formule de Borda du pendule simple est retrouvée : En effet, les calculs montrent que

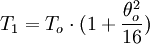
On trouve aussi les formules du ressort mou, ou du ressort dur. On pourra aussi tester les développements limités des formules exactes des puits de potentiel précédents.