Puits de potentiel - Définition

Introduction

Puits de potentiel unidimensionnel

Un puits de potentiel désigne, en physique, le voisinage d'un minimum local d'énergie potentielle.

Étude mathématique

Soit une courbe plane, située dans un plan vertical, en forme de cuvette. Un point matériel, de masse m, s'y meut, en glissant sans frottement. La conservation de l'énergie donne, en prenant l'abscisse curviligne s(t) comme inconnue, l'équation du mouvement de ce point:

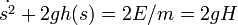
qui s'appelle en mathématiques une équation différentielle de Leibniz, liée à l'équation différentielle de Newton du second ordre :

.

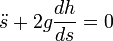
De l'équation de Leibniz, on tire la vitesse v(s)= ±

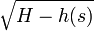
Ce qui ramène à l'étude d'un diagramme horaire. Par exemple le cas simple (dit de Torricelli) de h(s)=|s| y est étudié.

Il arrive que l'on considère en physique une équation similaire : le mouvement d'un point matériel sur un axe x'Ox, sous l'action d'une force F(x) :

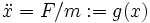
(On appelle énergie potentielle V(x) est l'opposée de la primitive de F(x)). La conservation de l'énergie donne le même type d'équation de Leibniz. On dit alors que la particule est confinée dans un puits de potentiel, sur l'intervalle [a,b], a et b, racines contiguës de V(x)= E.

Exemple : la cycloïde de Huygens (1659)

Huygens a trouvé quelle devait être la forme de la courbe pour que les oscillations soient isochrones : il fallait une cuvette qui se relevât plus vite que le cercle osculateur en O, de rayon R ; il trouva que la cycloïde convenait. Alors .

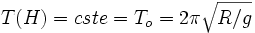
Le phénomène est tout à fait extraordinaire et splendide à regarder avec 2 cycloïdes identiques, parallèles, de R = 4 mètres, d'envergure 12.5m environ. Il est aussi très somptueux de procéder avec une troisième cycloïde, de R = 1m :

Une joue étant celle de la première cycloïde et l'autre celle de la troisième, le signal entendu est tic-tac-tic---toc---tic-tac-tic---toc, de période 3s environ , ceci quelle que soit l'envergure du mouvement, depuis environ 10 cm jusqu'à quelques m: c'est assez extraordinaire à voir et entendre. Pour le montage, on aura soin de calculer la bonne longueur de la suspension bifilaire associée à la masse d'environ 1 kg (détails techniques : penser à l'ajustement compte-tenu de l'effet pendule-double ; sinon, il faut que la masse soit un disque monté sur d'excellents roulements à bille, dont l'axe sera serti dans une perle oblongue passée dans le bi-fil. De plus, il faut évidemment prendre du fil INEXTENSIBLE, sous une charge de 3 kg. Enfin, il faut fixer solidement l'ensemble des joues pour éviter tout mouvement du support, en définitive assez lourd).

Cuvette symétrique

Soit l'origine O, au fond de la cuvette, sans restriction de généralité. Soit A le point d'abscisse s = a telle que h(A)= H.

Le mouvement se décrit qualitativement fort bien : la vitesse, maximale en O, ne cesse de décroître jusqu'à l'arrivée en A, au temps t1. Puis la particule rétrograde selon le même mouvement, et arrive en O, avec la vitesse opposée. Elle décrit alors l'autre bord de la cuvette, symétriquement, jusqu'au point symétrique A' et revient : le mouvement est périodique de période T = 4 t1. La méthode du diagramme horaire s'applique bien à ce cas qui peut donc s'expliquer et s'expérimenter sans de hautes mathématiques ; on peut ainsi tracer T(H).

Quelques cas de cuvettes symétriques

• La cuvette soliton : U(x) = -g²/ch²x

On trouve : x(t) = argsh [sha.sin wt] ; avec sha = sqrt[(g²+E)/(-E)] et la période T(E) = sqrt(2).Pi/ sqrt(-E)

• la cuvette soliton modifiée : U(x) = g²/sin²(x)

On trouve : x(t) =arc cos (cosa .cos wt) avec cosa = sqrt(1-g²/E) et la période T(E) = sqrt(2)Pi/sqrt(E)

• la cuvette de Jacobi : U(x) = g²/sn(x,k)

On trouve la période T = 4/c K(k") avec c²= 2(E-g²k²) et k" =k²(E-g²)/(E-g²k²), K(k) étant la fonction elliptique de première espèce.

• la cuvette U(x) =g².ch(2x) :

On trouve la période d'oscillation T = 4/a K(k) , avec a = sqrt(E+g²) et k² = (E-g²)/(E+g²)

• Remarque : par symétrie de Corinne, à ces cuvettes correspondent des barrière de potentiel, dont on peut évaluer en mécanique quantique l'effet tunnel ; c'est une des raisons de trouver un maximum d'exemples pour pouvoir interpréter nombre d'expériences.