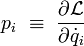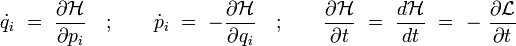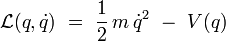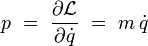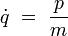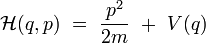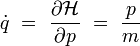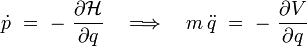Mécanique hamiltonienne - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La mécanique hamiltonienne, inventée par Hamilton en 1833, est une reformulation de la mécanique classique. Son formalisme a facilité l'élaboration théorique de la mécanique quantique.
Équations canoniques de Hamilton
Rappels de mécanique lagrangienne
En mécanique lagrangienne, les équations du mouvement d'un système à N degrés de liberté dépendent des coordonnées généralisées
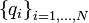
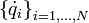
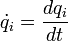
Le lagrangien peut donc s'écrire formellement comme une fonction :
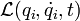
Moment conjugué
En mécanique hamiltonienne, chaque vitesse généralisée est remplacée par la quantité de mouvement associée, aussi appelée moment conjugué ou encore impulsion généralisée :
|
|
En coordonnées cartésiennes, les quantités de mouvement sont équivalentes aux moments linéaires, alors qu'en coordonnées polaires elles correspondent aux moments angulaires. Lorsque les coordonnées généralisées sont choisies arbitrairement, il n'est plus possible de donner une interprétation intuitive aux moments conjugués.
Hamiltonien
L'hamiltonien

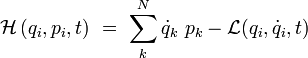
|
Dans le membre de droite de cette formule, les vitesses sont supposées être exprimées en fonction des moments conjugués.
Si les équations qui définissent les coordonnées généralisées sont indépendantes du temps t, on peut montrer que

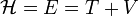
Équations canoniques de Hamilton
Sous forme différentielle, les deux membres de la définition de

![\begin{matrix} d \mathcal{H} &=& \sum_i \left[ \left({\partial \mathcal{H} \over \partial q_i}\right) dq_i + \left({\partial \mathcal{H} \over \partial p_i}\right) dp_i\right] + \left({\partial \mathcal{H} \over \partial t}\right) dt \\ d \mathcal{H} &=& \sum_i \left[ \dot{q}_i dp_i + p_i d\dot{q}_i - \left({\partial \mathcal{L} \over \partial q_i}\right) dq_i - \left({\partial \mathcal{L} \over \partial \dot{q}_i}\right) d\dot{q}_i \right] - \left({\partial \mathcal{L} \over \partial t}\right) dt \end{matrix}](https://static.techno-science.net/illustration/Definitions/autres/d/dae9418c172476ada73f9109c7fd8f06_692a658b846516bd75f38bfd1222f1d1.png)
|
En utilisant la définition des moments conjugués donnée précédemment et les équations d'Euler Lagrange traduisant le principe de l'action minimale du lagrangien, on obtient les équations du mouvement de Hamilton, dites équations canoniques de Hamilton :
|
|
Note: l'égalité
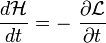
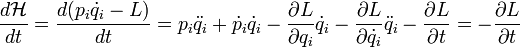
Où on a utilisé pour la dernière égalité la définition des moments conjugués.
Les équations de Hamilton sont des équations différentielles du premier ordre et donc plus faciles à résoudre que les équations de Lagrange qui sont du second ordre. Néanmoins, les étapes qui conduisent à ces équations sont plus complexes que celles de la mécanique lagrangienne : à partir des coordonnées généralisées et du lagrangien, il faut calculer l'hamiltonien, exprimer les vitesses généralisées en fonction des moments conjugués et remplacer celles-ci dans la définition de l'hamiltonien.
La méthode de Lagrange est moins lourde en termes de manipulations mathématiques. L'avantage principal de l'approche hamiltonienne est de fournir, grâce à la simplicité de son formalisme, un fondement théorique en mécanique. Par exemple, la mécanique quantique utilise un formalisme basé sur celui de la mécanique hamiltonienne.
On pourra aussi noter une certaine similitude entre les équations canoniques de Hamilton et les équations de Maxwell.
Exemple élémentaire : la particule non relativiste sur un axe
Soit une particule non relativiste de masse m se déplaçant sur un axe. On repère la position de cette particule par une coordonnée q. Supposons de plus que la particule est soumise à une force qui dérive de l'énergie potentielle V(q). Le lagrangien s'écrit alors :
|
|
Le moment conjugué vaut alors :
|
|
il s'identifie à la quantité de mouvement habituelle. Cette formule peut être inversée :
|
|
On obtient alors le hamiltonien par transformée de Legendre :
|
|
Les équations canoniques conduisent alors à :
|
|
et à l'équation de la dynamique de Newton :
|
|