Représentation induite d'un groupe fini - Définition

Propriétés

Premières propriétés

Les représentations induites héritent ce certaines propriétés immédiates :

• Soit (W, θ) une représentation du sous-groupe H, (V, ρ) la représentation induite sur G et E un sous-espace stable de ρ. Alors la restriction de ρ à E est induite par la restriction de θ à E.

En effet, soient c une classe à gauche, W_c l'image de W à gauche par ρ_s si s est un élément de c et E_c l'intersection de W_c et E. Les intersections deux à deux des E_c, si c décrit l'ensemble des classes à gauche est réduite au vecteur nulle car celles des W_c le sont. Leur somme génère bien l'espace E car celle des W_c est égale à V, ce qui démontre la proposition.

• Soient (W₁, θ₁) et (W₂, θ₂) deux représentations de H, (V₁, ρ₁) et (V₂, ρ₂) deux représentations de G induites par les précédentes, alors la représentation somme directe de V₁ et V₂ est induite par la représentation somme directe de W₁ et W₂.

La démonstration est analogue à la précédente.

Il existe une propriété fondamentale sur les représentations induites :

• Il existe une et une seule représentation induite de G par (W, θ) à un isomorphisme près.

Si W est identifié à un H-module et si (V, ρ) est la représentation induite, alors, en identifiant V à un K[G]-module, on obtient l'égalité tensorielle :

De plus la structure d'origine et celle induite disposent d'une analogie forte :

• Si (V, ρ) est la représentation induite par (W, θ) et si (E, σ) est une représentation de G, les deux algèbres Hom^H (W, Res E) et Hom^G (V, E) sont isomorphes.

Cette propriété est l'équivalence, entre terme de morphismes de la loi de réciprocité de Frobenius.

L'utilisation des G-modules et du produit tensoriel montre de manière naturelle l'existence et l'unicité de la représentation induite :

• K[G] est une représentation de G induite par K[H].

Il suffit pour cela de remarquer que K[G] est un K[H] de base C si C est un système de représentants des classes à gauche de H dans G. Soit s un élément de C, K[H].s est l'image de K[H].1 par l'application linéaire qui à h élément de K[H] associe h.s, c’est-à-dire l'image de K[H].1 par le point s de la représentation. Le fait que les K[H].s soit une somme directe égale à K[G] est la conséquence du fait que C est une base.

Si (W, θ) est une représentation de H, alors W est un K[H]-module. Considérons alors le produit tensoriel de W et de K[G], tout deux considérés comme des K[H]-modules :

Ce produit tensoriel I correspond au module déduit de W par extension des scalaires K[H] à K[G].

• Le module I est la représentation induite de G par (W, θ).

En effet, W' est isomorphe à W en tant que K espace vectoriel et la représentation θ est isomorphe à la représentation multiplication externe par un élément de H. Soit c un élément de C, c.W' forme bien une somme directe égale à I, ce qui démontre que la représentation est bien induite.

Soit V un espace vectoriel contenant W et ρ une représentation tel que la restriction de ρ à W soit égal à θ. Considérons alors l'injection canonique de W dans V, elle se prolonge par linéarité en une application linéaire φ de I dans V. L'application φ est alors un morphisme de K[G]-module.

• (V, ρ) est une représentation induite par (W, θ) si et seulement si φ est une bijection.

Cette proposition découle directement du fait que C est une base de K[G] en tant que K[H]-module.

On en déduit la conséquence suivante :

• Il existe une et une seule représentation induite de G par (W, θ) à un isomorphisme près.

On dispose de la propriété :

• Si (V, ρ) est la représentation induite par (W, θ) et si (E, σ) est une représentation de G, les deux algèbres Hom^H (W, Res E) et Hom^G (V, E) sont isomorphes.

En effet, considérons l'application de Hom^H (W, Res E) dans Hom^G (V, E), qui au morphisme f associe 1_K[G] f. Cette application est bien un morphisme d'algèbre, son noyau est manifestement réduit au vecteur nul.

Montrons qu'il est surjectif, soit g un morphisme de Hom^G (V, E), g et (1_K[G] w_i) une base de I en tant que K[G]-module. Si φ désigne toujours l'isomorphisme entre I et V, alors g est défini par l'image de la base (φ(1_K[G] w_i)) et l'application de W dans E, qui à w_i associe g (φ(1_K[G] w_i)) est bien l'antécédent dans Hom^H (W, Res E) de g, ce qui termine la démonstration.

 

Critère d'irréductibilité de Mackey

Une double application de la formule de réciprocité de Frobenius décrite ci dessous permet de démontrer le résultat suivant, connu sous le nom de critère d'irréductibilité de Mackey. Quelques définitions sont nécessaire pour l'exprimer. H_t désigne ici le sous-groupe intersection du sous-groupe conjugué de H par t avec S, et si t est un élément de G, θ^t désigne la représentation de H_t dans W définie par :

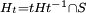
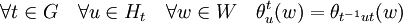
Le critère s'applique avec une double classe sur H.

Il s'énonce de la manière suivante :

• La représentation (V, ρ) est irréductible si et seulement si θ^s et la restriction de θ à H_s sont disjointes quand s est un élément de G - H.

Il existe un corollaire, dans le cas où le groupe H est distingué :

• La représentation induite de G par celle de H (W, θ) est irréductible si et seulement si (W, θ) est irréductible et n'est isomorphe à aucune représentation conjuguée θ^s.

Les définitions utilisées et les démonstrations sont présentes dans l'article associé.