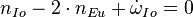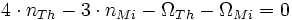Résonance orbitale - Définition

Introduction

Une résonance orbitale, en astronomie, a lieu lorsque deux objets orbitant autour d'un troisième ont des périodes de révolution dont le rapport est une fraction entière simple. C'est un cas particulier de résonance mécanique. Par exemple, Pluton est en résonance 2:3 avec Neptune c'est-à-dire que Pluton effectue deux révolutions autour du Soleil pendant que Neptune en réalise trois. Cette résonance est stable : une perturbation de l'orbite de Pluton serait corrigée par l'attraction de Neptune

Stabilité des orbites

Depuis la publication de lois de Newton, le problème de stabilité des orbites a préoccupé beaucoup de mathématiciens, en commençant par Laplace. Comme la solution du problème de deux corps ne prend pas en compte les interactions mutuelles entre les planètes, de petites interactions vont sûrement s’accumuler et finir par changer les orbites. Ou alors, il reste à découvrir de nouveaux mécanismes qui maintiennent la stabilité de l’ensemble. C’était aussi Laplace qui a trouvé les premières réponses pour expliquer la remarquable danse des lunes de Jupiter. On peut dire que ce champ d’investigation est resté très actif depuis et il reste toujours des mystères à élucider (par exemple les interactions des petites lunes avec les particules des anneaux des planètes géantes).

En général, la résonance peut :

• concerner soit un seul paramètre, soit n’importe quelle combinaison des paramètres d’orbite ;
• agir sur des échelles de temps très différentes, comparables avec les périodes des orbites, ou séculaires, allant jusqu’à 10⁴ - 10⁶ d’années ;
• elle peut tout aussi bien être la cause de la stabilité des orbites que celle de leur déstabilisation.

Commensurabilité des périodes de révolution

Il n’existe que cinq résonances de ce type concernant les planètes ou les lunes majeures dans le système solaire (un bien plus grand nombre concernant les astéroïdes, les anneaux et les petits satellites) :

• 2:3 Neptune-Pluton ; Neptune-(32929) 1995 QY₉ ; Neptune-(90482) Orcus ; Neptune-(28978) Ixion. Ils forment les Plutino
• 4:2 Mimas-Téthys (lunes de Saturne) ;
• 2:1 Encelade-Dioné (lunes de Saturne) ;
• 4:3 Titan-Hypérion (lunes de Saturne) ;
• 1:2:4 Io-Europe-Ganymède (lunes de Jupiter), l'unique résonance de Laplace.
• 1:2 Neptune-(20161) 1996 TR₆₆ ; Neptune-(26308) 1998 SM₁₆₅; Neptune-1997 SZ₁₀; Neptune-1999 RB₂₁₆; Neptune-(130391) 2000 JG₈₁; Neptune-(119979) 2002 WC₁₉. Ils forment les Twotino.

Les simples relations entières entre les périodes de révolution cachent des relations plus complexes :

• les points de conjonction peuvent osciller autour des valeurs d’équilibre définis par la résonance ;
• compte tenu des excentricités des orbites, les nœuds ou les périastres peuvent changer.

Comme une illustration, pour la très connue résonance 1:2 Io-Europe, si les périodes de révolution étaient réellement dans ce rapport exact, les mouvements moyens (inverse de la période) satisferaient l’équation suivante : :

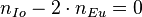
Toutefois, en vérifiant avec les données on obtient − 0.7395^ojour ^{− 1}, une valeur bien trop grande pour être négligée.

En fait, la résonance est exacte mais elle doit inclure aussi la précession du périastre L’équation corrigée (qui fait partie des relations de Laplace) est

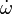
En d’autres termes, le mouvement moyen de Io est bien le double de celui d’Europe en tenant compte de la précession du périastre. Un observateur situé sur le périastre aurait vu les lunes arrivant à la conjonction au même endroit. Les autres résonances satisfont les équations similaires à l’exception de la paire Mimas-Téthys. Dans ce dernier cas, la résonance satisfait l’expression suivante

Le point de conjonction oscille autour d’un point à mi-chemin entre les nœuds des deux lunes.

La résonance de Laplace

La résonance la plus remarquable, celle de trois lunes Galiléennes, inclut la relation qui contraint la position des lunes sur leurs orbites :

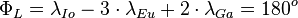
où λ sont les longitudes moyennes des lunes. Cette contrainte rend impossible une triple conjonction des lunes. Le graphique illustre les positions des lunes après 1, 2 et 3 périodes de Io.