Résonance - Définition

Introduction

La résonance est un phénomène selon lequel certains systèmes physiques (électriques, mécaniques...) sont sensibles à certaines fréquences. Un système résonant peut accumuler une énergie, si celle-ci est appliquée sous forme périodique, et proche d'une fréquence dite « fréquence de résonance » ou « fréquence naturelle » ou fréquence propre. Soumis à une telle excitation, le système va être le siège d'oscillations de plus en plus importantes, jusqu'à atteindre un régime d'équilibre qui dépend des éléments dissipatifs du système, ou bien jusqu'à une rupture d'un composant du système.

Si on soumet un système résonant à un degré de liberté non plus à une excitation périodique mais à une percussion (pour les systèmes mécaniques), ou à une impulsion (pour les systèmes électriques), alors le système sera le siège d'oscillations amorties, sur une fréquence dite fréquence propre et retournera progressivement à son état stable.

Les domaines où la résonance intervient sont innombrables : balançoire enfantine, mais aussi résonances acoustiques des instruments de musique, la résonance des marées, la résonance orbitale en astronomie, la résonance de la membrane basilaire dans le phénomène d'audition, les résonances dans des circuits électroniques et, pour finir tous les systèmes, montages, pièces mécaniques sont soumis au phénomène de résonance. Les systèmes abstraits sont également soumis à des résonances, par exemple la dynamique des populations.

Notions de base

Principe physique

Un système susceptible d'entrer en résonance, c'est-à-dire susceptible d'être le siège d'oscillations amorties, est un oscillateur. Un tel système a la particularité de pouvoir emmagasiner temporairement de l'énergie sous deux formes : potentielle ou cinétique. L'oscillation est le phénomène par lequel l'énergie du système passe d'une forme à l'autre, de façon périodique.

Par exemple, dans un système mécanique, l'énergie passe de la forme potentielle à la forme cinétique : une corde vibrante aura son énergie sous forme entièrement potentielle au moment où elle passe par son maximum d'élongation. Au moment où la corde passe par sa position d'équilibre, sa vitesse est maximale, et son énergie est entièrement sous forme cinétique.

Dans un circuit LC, l'énergie est sous forme potentielle quand la tension est maximale aux bornes du condensateur. L'énergie est sous forme cinétique (ou magnétique) quand le courant est maximum dans la bobine (et la tension nulle sur le condensateur).

Si on injecte une énergie potentielle au moment où l'énergie potentielle déjà emmagasinée est maximale, l'énergie ainsi injectée s'ajoute à l'énergie déjà emmagasinée et l'amplitude de l'oscillation va augmenter, ainsi que l'énergie totale. De la même façon, si on injecte de l'énergie cinétique au moment où l'énergie cinétique est maximale, l'énergie totale augmentera. Si on apporte ainsi de l'énergie avec une périodicité égale (ou proche) de la périodicité propre du système, l'énergie totale va augmenter régulièrement. L'amplitude des oscillations du système va ainsi croître. L'exemple le plus simple est celui d'une balançoire : l'énergie de chaque poussée s'ajoute à l'énergie totale, à condition de pousser au bon moment...

Le phénomène de résonance n'est rien d'autre que cet effet d'accumulation de l'énergie en injectant celle-ci au moment où elle peut s'ajouter à l'énergie déjà accumulée, c'est-à-dire « en phase » avec cette dernière.

Amortissement

Quand l'excitation aura cessé, le système résonant va être le siège d'oscillations amorties : il va revenir plus ou moins vite à son état d'équilibre stable. En effet, l'énergie de départ sera peu à peu absorbée par les éléments « dissipatifs » du système (amortisseur visqueux en mécanique, résistances en électricité...). Un système peu amorti sera le siège d'un grand nombre d'oscillations qui diminueront lentement avant de disparaître complètement.

Si on soumet un système peu amorti à une excitation périodique permanente selon sa fréquence de résonance, l'énergie ainsi apportée va s'accumuler lentement et se traduira par des oscillations de grande amplitude. En régime stabilisé, l'énergie apportée à chaque période est égale à l'énergie dissipée, ce qui explique la grande amplitude des oscillations du système peu amorti. L'énergie accumulée sera importante, mais un amortissement accru peut diminuer l'amplitude des oscillations, l'énergie dissipée par période et donc l'énergie accumulée.

En électricité, on peut chiffrer l'amortissement en définissant le « coefficient de surtension » ou la « sélectivité ».

Modes propres

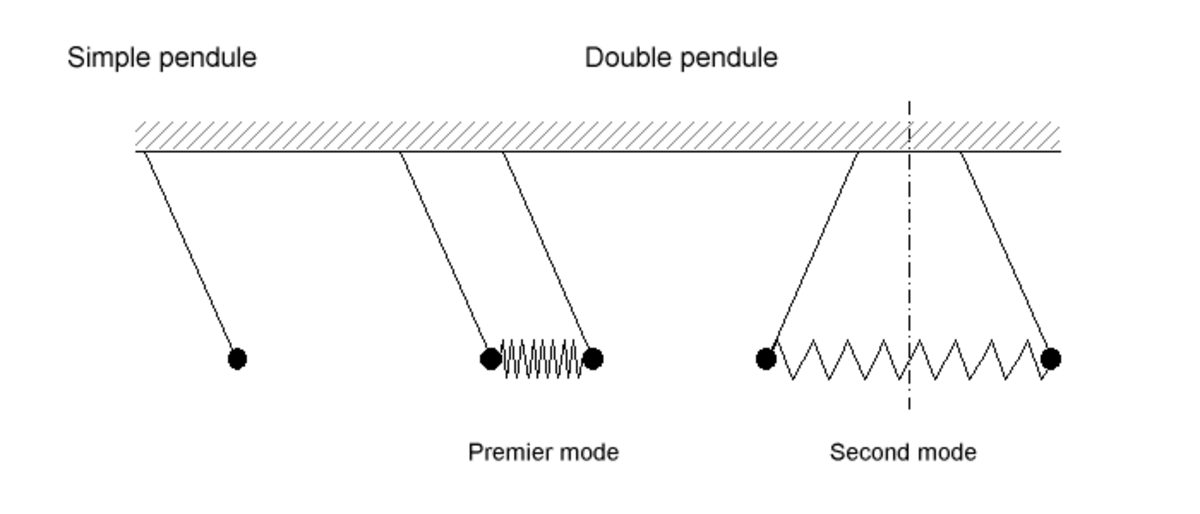
Implicitement, l'introduction concerne des systèmes à un degré de liberté ou supposés tels dont l'évolution est décrite par un seul paramètre fonction du temps. On rencontre de tels systèmes, entre autres, en mécanique avec le simple pendule ou le système masse-ressort, en électricité avec le circuit RLC. Leurs oscillations libres ne peuvent se produire qu'à une fréquence bien définie susceptible d'induire une résonance.

Si on couple deux pendules par un ressort, le système est alors décrit par les inclinaisons généralement distinctes des deux pendules. Ce système à deux degrés de liberté possède deux modes propres dans lesquels les pendules oscillent à la même fréquence. Toute oscillation libre est une somme des deux modes propres correspondants et, face à une excitation sinusoïdale, chacun d'eux peut engendrer une résonance. En supposant les deux pendules identiques, l'origine des deux types d'oscillation devient évidente. Dans un cas les pendules oscillent de concert, comme s'ils étaient liés par une barre rigide ; la fréquence propre du système est la même que celle du pendule simple. Dans l'autre, ils oscillent en opposition, comme si le milieu du ressort avait été fixé ; une moitié de ressort accroît donc la raideur associée à chacun d'eux, ce qui, comme il est précisé plus loin, augmente la fréquence propre.

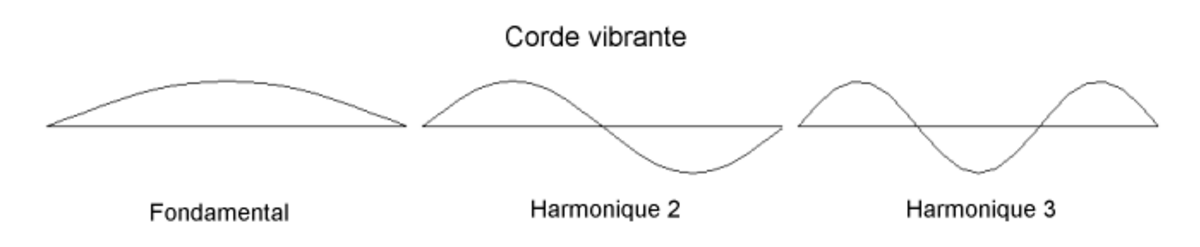
Ces remarques se généralisent à des systèmes qui possèdent un nombre quelconque de degrés de liberté. La déformée d'une corde vibrante ou d'une poutre élastique est caractérisée par une infinité de positions ; il s'agit alors de systèmes continus à une infinité de degrés de liberté possédant une infinité de modes propres. Dans le cas de la corde sans raideur en flexion, les modes propres ont des formes sinusoïdales (pour plus de précisions, voir Onde sur une corde vibrante. La plus basse fréquence est alors appelée fréquence fondamentale tandis que les harmoniques ont des fréquences multiples de celle-ci, le spectre est l'ensemble des fréquences propres.

Animation : 3 premiers modes de vibration d'une corde

Généralement, l'importance relative de l'amortissement s'accroît à mesure que s'élève l'ordre des modes, ce qui fait qu'il est suffisant de s'intéresser aux tous premiers modes, dans les problèmes techniques si ce n'est en musique.

La représentation modale est pertinente dans le domaine des basses fréquences, c'est-à-dire pour les premiers modes propres (les modes sont classés traditionnellement par fréquences propres croissantes sur le spectre). Dans les domaines moyenne et haute fréquence,on utilise des méthodes adaptées à la densité spectrale élevée. Les domaines moyenne fréquence et haute fréquence sont définis par la densité spectrale. En effet, l'expression en fréquences n'a pas de sens pour définir ces domaines, une similitude sur un système physique modifie les fréquences propres mais le spectre reste semblable, à un facteur près. Dans le cas de fréquences multiples, il existe un sous-espace propre donc les modes propres sont arbitraires dans ce sous espace. Dans le cas de fréquences voisines (densité spectrale élevée), la représentation modale n'est pas robuste car de faibles perturbations du domaine physique vont entraîner un changement important des modes propres associés à ces fréquences. Donc la représentation modale n'est pertinente que pour le domaine des basses fréquences, domaine défini par la densité spectrale. Le domaine basse fréquence s'étendra jusqu'à quelques Hz en génie civil, jusqu'à des milliers de Hz pour de petites structures mécaniques.

Réponse à une excitation

Dans un système oscillant à un degré de liberté, on constate que le rapport de l'amplitude X de la réponse à l'amplitude F de l'excitation dépend de la masse M (ou inertie ou, en électricité, auto-inductance), de la raideur K (ou inverse de la capacité) et de l'amortissement B (ou résistance) :

Cette formule montre, ce qui se généralise qualitativement à des systèmes beaucoup plus complexes, voire non-linéaires, que la fréquence propre croît avec la raideur et décroît lorsque l'inertie augmente.

Quantitativement, pour un système linéaire, la généralisation se ferait en définissant un effort généralisé, en projetant les efforts extérieurs sur le mode concerné. Un mode n'est pas excitable sur les nœuds de vibration.

L'amplification ne varie pas seulement en fonction de la fréquence. Elle dépend également de l'amortissement du système : lorsque celui-ci décroît, l'amplification augmente dans une bande de fréquences de plus en plus étroite.

Ce phénomène d'amplification est mis à profit dans divers domaines pour séparer une fréquence déterminée de ses voisines.

À l'inverse, il peut être fréquemment à l'origine de dommages causés au système. Dans ce dernier cas, on cherche soit à l'atténuer en augmentant l'amortissement, soit à déplacer la fréquence propre en jouant sur l'inertie ou sur la raideur.

La synchronisation

Christian Huygens a remarqué que deux horloges à balancier, placées sur la même cloison, synchronisaient leur mouvement ; il en a fourni l'explication. Le système composé des deux balanciers et de la cloison a deux fréquences voisines faiblement couplées, il possède par le couplage deux modes propres correspondant aux mouvements en phase et en opposition de phase des deux pendules : c'est sur le premier mode que se produit la synchronisation. On retrouve la synchronisation dans de nombreux phénomènes naturels : vols d'oiseau, clignotement des lucioles...