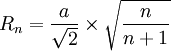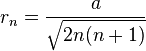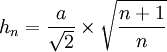Simplexe - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Propriétés
- Tout n-x simplexe généré par un sous-ensemble de {a, a, ..., a} (qui sont les différents sommets du simplexe) est appelé n-x face de s.
- L'ensemble des faces de s différentes de s lui-même sont appelées faces propres de s, et leur union est appelée bord de s.
- Un n simplexe n'a pas de diagonales (voir diagonale), car par définition, tous les (n+1) sommets d'un n simplexe sont déjà reliés entre eux.
- L'isobarycentre d'un n simplexe est situé à
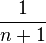
- Un simplexe est son propre dual (voir dualité), ce qui signifie que lorsque l'on relie entre eux tous les centres des (n-1)faces d'un n simplexe, on retombe sur le même simplexe, réduit d'un demi.
- Si un simplexe possède un "coin droit" (c'est-à-dire que toutes les arêtes se rencontrant en un sommet sont perpendiculaires en elles), on peut alors utiliser la généralisation en n dimensions du théorème de Pythagore : "La somme des carrés des (n-1) volumes des hyperfaces adjacentes au coin droit est égale au carré du (n-1) volume opposé au coin droit". Par exemple, dans un triangle ABC rectangle en A on aura BC2 = AB2 + AC2, dans une pyramide ABCD rectangle en A on aura BCD2 = ABC2 + ABD2 + ACD2, et dans un pentatope ABCDE rectangle en A on aura BCDE2 = ABCD2 + ABCE2 + ABDE2 + ACDE2.
- Topologiquement, un n simplexe est homéomorphe (voir homéomorphisme) à une n sphère. Chaque n simplexe est une variété convexe sans trous ayant n dimensions. La caractéristique d'Euler de n'importe quel n simplexe vaudra donc 0 si n est pair et 2 si n est impair, comme pour la n sphère.
- Le groupe des isométries d'un n simplexe régulier est d'ordre n!.
Formules de longueurs remarquables et des n-volumes
- Chaque simplexe possède un hypervolume qui correspond à son intérieur (pour le segment il s'agit de sa longueur, pour le triangle de son aire, pour le tétraèdre de son volume). On note le n volume d'un n simplexe Vn, pour tout simplexe régulier d'arête a il vaut :
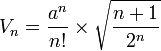
Cette formule est obtenue pour un simplexe par récurrence à partir du simplexe de dimension précédente, en effet, le n volume d'un n simplexe est le produit d'une hauteur (distance entre un sommet et le centre de la (n-1)face opposée) et de la base correspondante ((n-1) volume d'une (n-1)face), divisé par le nombre de dimensions du simplexe :
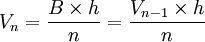
Exemples :
-
- La longueur d'un segment est donc de V1 = a
- L'aire du triangle équilatéral est de
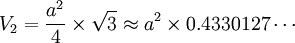
- Le volume du tétraèdre régulier est de
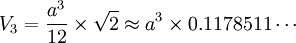
- L'hypervolume du pentachore régulier est de
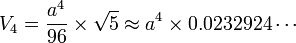
- La longueur d'un segment est donc de V1 = a
- Soit hn la hauteur du n simplexe, Rn le rayon de l'hypersphère circonscrite au n simplexe, et rn le rayon de l'hypersphère inscrite au n simplexe, on a alors :
-
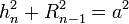
-
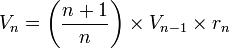
-
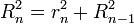
-
- Par récurrence, en partant des valeurs V1 = h1 = 1 et
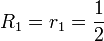
-