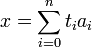Simplexe - Définition

Introduction

Un tétraèdre est un 3-simplexe

En mathématiques, et plus particulièrement en géométrie, un simplexe est une généralisation du triangle à une dimension quelconque.

Définition

Le repère, dans l'espace à 3 dimensions, est formé des 4 sommets d'un tétraèdre, donc de 3 axes

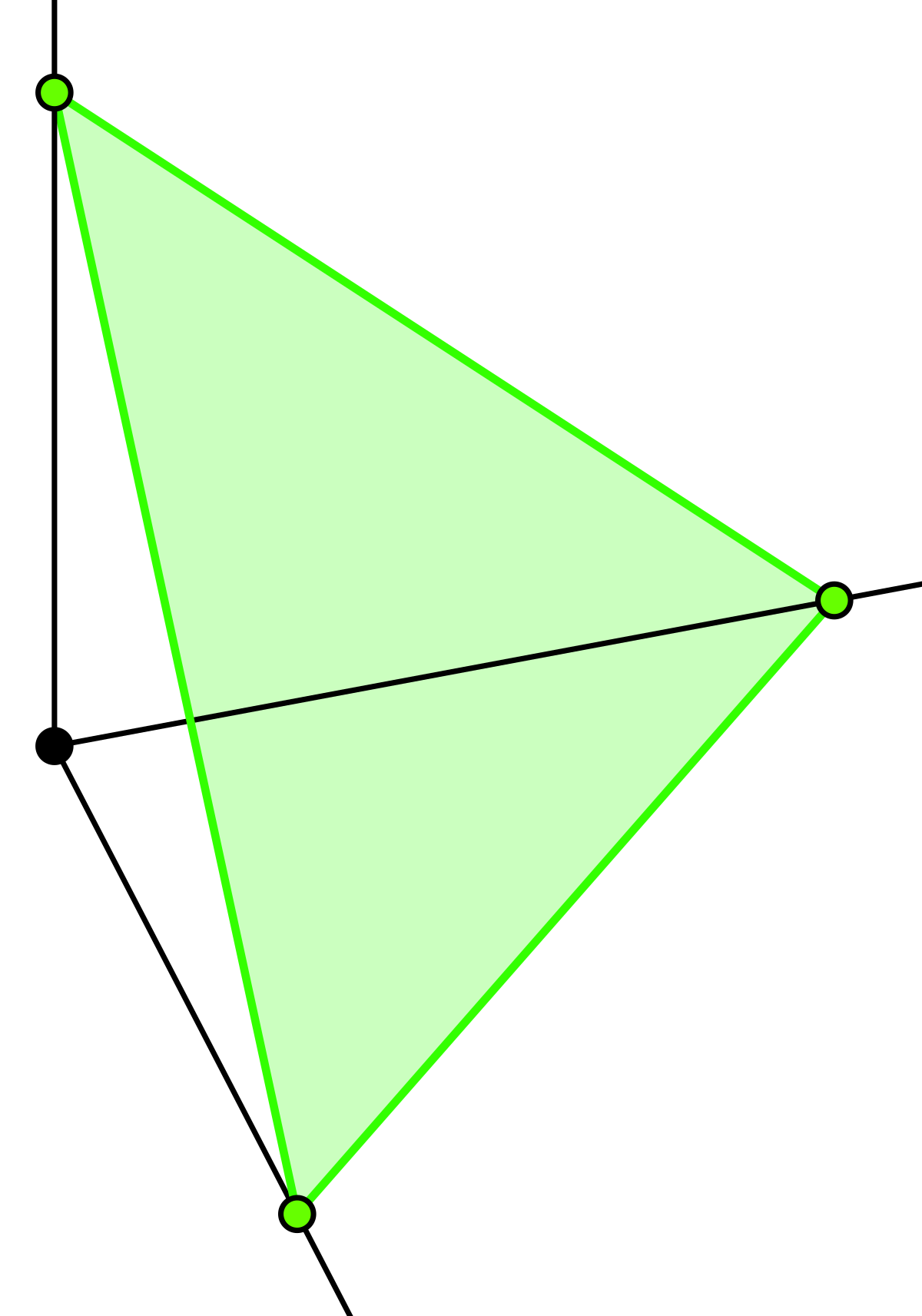
En géométrie, un simplexe ou n simplexe est l'analogue à n dimensions du triangle. Un simplexe tire son nom du fait qu'il soit l'objet géométrique clos le plus "simple" qui a n dimensions, par exemple sur une droite (1 dimension) l'objet le plus simple à 1 dimension est le segment, alors que dans le plan (2 dimensions) l'objet le plus simple à 2 dimensions est le triangle, et dans l'espace (3 dimensions) l'objet le plus simple à 3 dimensions est le tétraèdre (pyramide à base triangulaire).

Plus exactement, un simplexe est l'enveloppe convexe d'un ensemble de (n+1) points utilisé pour former un repère affine dans un espace euclidien de dimension n, ce qui signifie que :

• sur une droite le repère sera fait d'une origine et de 1 point (généralement un repère (O,I), définissant l'unité de l'axe), et [OI] est un segment.
• dans le plan le repère sera fait d'une origine et de 2 points (généralement un repère (O,I,J), définissant l'unité pour chaque axe), et OIJ est un triangle.
• dans l'espace le repère sera fait d'une origine et de 3 points (généralement un repère (O,I,J,K), définissant l'unité pour chaque axe), et OIJK est un tétraèdre.

Les coordonnées des sommets du simplexe (dans le repère formé de ses sommets) sont alors :

e = (1, 0, 0, 0, …, 0),

e = (0, 1, 0, 0, …, 0),

e = (0, 0, 1, 0, …, 0),

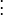
e = (0, 0, 0, 0, …, 1)

Le nombre n est appelé la dimension ou degré ou même l'ordre du n simplexe s. Par exemple, un 0 simplexe est un point, un 1 simplexe est un segment, un 2 simplexe est un triangle, un 3 simplexe est un tétraèdre, un 4 simplexe est un pentachore (ou pentatope), etc... Comme le simplexe à 0 dimension est déjà le point (qui n'est pas rien, car il existe), on utilise alors pour signaler qu'il n'y a rien du tout, la dimension -1, qui n'a qu'un sens théorique.

Soit donc s un simplexe formé par les point a, ..., a, x un point de s, on peut écrire de manière unique:

où les t sont les coordonnées barycentriques de x relative à a, ..., a. On remarque la ressemblance entre cette formule et celle de l'équilibre d'un objet en physique mécanique statique : , qui dit que la somme des forces extérieures appliquées à un objet en équilibre est égale au vecteur nul. Cela vient du fait que l'objet, quel que soit l'intensité de ces n forces qui le tirent (qu'on peut se représenter comme n ressorts attachés à l'objet et aux n sommets d'un (n-1) simplexe), restera toujours dans ce simplexe : tout point du simplexe peut être défini par ces forces qui l'attirent plus ou moins vers tel ou tel sommet, d'où l'utilisation de la notion de barycentre. On notera de plus que, pour qu'un objet soit en équilibre, il doit nécessairement se trouver dans le simplexe formé par les points qui l'attirent.

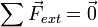
Un simplexe régulier est un simplexe qui est aussi un polytope régulier (c'est-à-dire que toutes ses arêtes sont de même longueur, que ses faces sont de même nature géométrique, et s'organisent de la même façon dans les mêmes quantités à chaque sommet).

Le mot "simplexe" a été donné par Pieter Hendrik Schoute en 1902, mais Ludwig Schläfli avait déjà démontré l'existence des simplexes réguliers pour tout dimension n (donc des simplexes tout court) lorsqu'il a prouvé qu'il y avait toujours au moins trois polytopes réguliers pour toute dimension supérieure à 3 (à savoir le n simplexe, ainsi que le n hypercube et le n hyperoctaèdre).