Simplexe - Définition
La liste des auteurs de cet article est disponible ici.
Représentations
Les n-simplexes ayant souvent plus de dimensions que les objets que nous sommes habitués à voir dans la vie courante, on utilise différents moyens de représentation pour travailler plus facilement avec. Parmi ces représentations, on utilise souvent les projections d'un n-simplexe dans un espace dimension inférieure (généralement 2 ou 3).
Il est impossible de représenter parfaitement un objet dans un espace qui a moins de dimensions que lui, donc il faut utiliser ces représentations avec prudence, certaines déforment les longueurs, les angles, voire la structure du simplexe, ou alors nous font voir des segments qui se croisent alors qu'en réalité ils ne se croisent pas.
Graphes
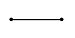
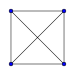
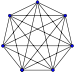
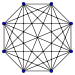
La représentation en deux dimensions d'un n simplexe est un graphe. Pour tracer le graphe d'un n simplexe, il suffit de relier tous entre eux n+1 points.
Quand on a affaire au graphe d'un simplexe dont on ne connaît pas le degré, il suffit de compter le nombre de segments qui sont reliés à un sommet.
Pour passer du graphe d'un n simplexe à celui d'un (n+1) simplexe, on ajoute un nouveau point et on relie tous les autres à celui-ci.
| Simplexe | Segment | Triangle | Tétraèdre | Pentatope | 5 simplexe | 6 simplexe | 7 simplexe |
|---|---|---|---|---|---|---|---|
| Dimension | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Sommets | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Graphe |
|

|
|

|

|
|
|
Attention : le graphe n'étant qu'une projection du n simplexe sur un plan, comme une ombre, les longueurs et les angles ne sont pas respectés : il faut s'imaginer que tous les segments sont de même longueur, et que tous les triangles qui relient 3 sommets sont équilatéraux si le simplexe est régulier. De plus, les diagonales du graphe ne se rencontrent jamais en réalité, mais passent devant ou derrière les autres.
Un graphe comme ceux-ci est aussi appelé polygone de Pétrie car il est obtenu par la projection orthogonale d'un polytope sur un plan.
Diagramme de Coxeter-Dynkin
Le diagramme de Coxeter-Dynkin d'un n simplexe est sous la forme :











Symbole de Schläfli
Le symbole de Schläfli d'un simplexe est sous la forme {3,3,3,...,3,3} (avec n-1 fois le nombre 3).
Eléments
Les éléments d'un simplexe sont appelés nfaces, où n est leur dimension :
- les 0faces sont appelées sommets
- les 1faces sont appelées arêtes
- les 2faces sont appelées faces
- les 3faces sont appelées cellules
L'ensemble des (n-1)faces d'un n simplexe forment son enveloppe.
Les nfaces d'un simplexe sont elles-mêmes des simplexes de dimensions inférieures. Par exemple, un tétraèdre aura des faces triangulaires.
Quand on liste les nfaces des simplexes ainsi que leur nombre, on obtient un triangle de Pascal :
| Simplexe | Nombre de sommets | Nombre d'arêtes | Nombre de faces | Nombre de cellules | Nombre de 4-faces | Nombre de 5-faces | Nombre de 6-faces |
|---|---|---|---|---|---|---|---|
| Point | 1 | - | - | - | - | - | - |
| Segment | 2 | 1 | - | - | - | - | - |
| Triangle | 3 | 3 | 1 | - | - | - | - |
| Tétraèdre | 4 | 6 | 4 | 1 | - | - | - |
| Pentachore | 5 | 10 | 10 | 5 | 1 | - | - |
| 5 simplexe | 6 | 15 | 20 | 15 | 6 | 1 | - |
| 6 simplexe | 7 | 21 | 35 | 35 | 21 | 7 | 1 |
| … |
Triangle de Pascal, dont une des caractéristique est que la seconde colonne corresponde à chaque nombre triangulaire, la troisième à chaque nombre tétraédrique, la quatrième à chaque nombre pentatopique...
Le nombre de sommets d'un n simplexe vaut N0 = n + 1, et le nombre de nfaces vaut toujours Nn = 1 car il s'agit du simplexe lui-même. Le nombre d'arêtes d'un n simplexe vaut
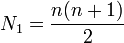
Entre les nombres de chaque élément d'un simplexe, il y a une relation d'Euler, dans laquelle en ajoutant les éléments de dimension paire (sommets, faces, 4faces, 6faces, ...), et en soustrayant les éléments de dimension impaire (arêtes, cellules, 5faces, 7faces, ...) on obtient la caractéristique d'Euler-Poincaré du simplexe, qui vaut 0 pour les simplexes de degré pair et 2 pour les simplexes de degré impair :
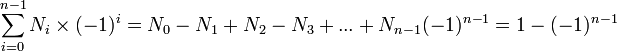
- Pour le segment : 2 points = 2
- Pour le triangle : 3 points - 3 arêtes = 0
- Pour le tétraèdre : 4 points - 6 arêtes + 4 faces = 2
- Pour le pentachore : 5 points - 10 arêtes + 10 faces - 5 cellules = 0