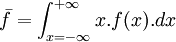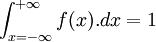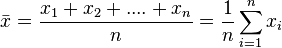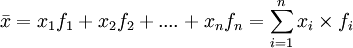Moyenne arithmétique - Définition
La moyenne arithmétique d'une série statistique est la moyenne ordinaire, c'est-à-dire le rapport de la somme d’une distribution d’un caractère statistique quantitatif discret par le nombre de valeurs dans la distribution.
Sa formulation mathématique peut se faire comme suit :
Pour une série statistique dont le nombre total d’occurrences est infini ou inconnu, mais dont les fréquences sont connues pour chaque valeur possible de la série, la formulation mathématique devient :
La moyenne arithmétique d'une distribution f d’une variable continue à valeur dans un intervalle scalaire fini [x0, x1] est la généralisation à la limite de la formule statistique discrète précédente :
-
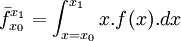
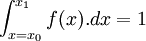
Sa dimension n'est pas une fréquence, mais celle de la variable continue.
Si la distribution f est définie sur toutes les valeurs réelles de sa variable continue, la moyenne arithmétique de la distribution est :
-